Image-based Personalised Models of Cardiac Electrophysiology for Ventricular Tachycardia Therapy Planning
1 Introduction
The muscular organ that beats in our chests has been recognised as vital by our ancestors long before the invention of writing. Home of the soul in the ancient Egyptian religion, object of interest for Greek philosophers, it took several centuries before its role (pumping blood, oxygen and nutrients throughout our bodies) stopped being debated. In the 21st century, it is the (almost) universal symbol of love; probably because of the very perceptible modifications of its pace when emotions overwhelm us, a consequence of its control by our autonomous nervous system.
This control is mediated by electrochemical reactions involving both the nervous and the cardiovascular system. Muscle cells, similarly to neurons, exhibit brief and localised but propagating perturbations of their transmembrane voltage, the action potentials. In the heart, the complex dynamics of this propagation are fundamental to its optimal1 contraction.
In this manuscript we will not directly focus on the pumping role of the heart, but rather on its electrical activity, i.e., on the signals that trigger its contraction.
1.1 Biomedical aspects
1.1.1 Cardiac Physiology
1.1.1.1 Pump function
Human hearts, like those of mammals and birds, are divided into four chambers. Two atria receive blood through the venous system and pump it into the ventricles through the mitral and tricuspid valves. Ventricles, in turn, eject it through the aortic and pulmonary valves to the rest of the body via the arterial network. Atria and ventricles are grouped two by two to form the right and left hearts. The former is responsible for pumping “used” blood to the lungs, where it releases carbon dioxide and fixes dioxygen. The latter pumps oxygen-rich blood to the organs that will use this gas as a source of energy.
The heart contraction ensures an efficient expulsion of the blood as it shortens along axes determined by the fibre orientation (fig. 2) of the heart muscle.
1.1.1.2 Sinus rhythm
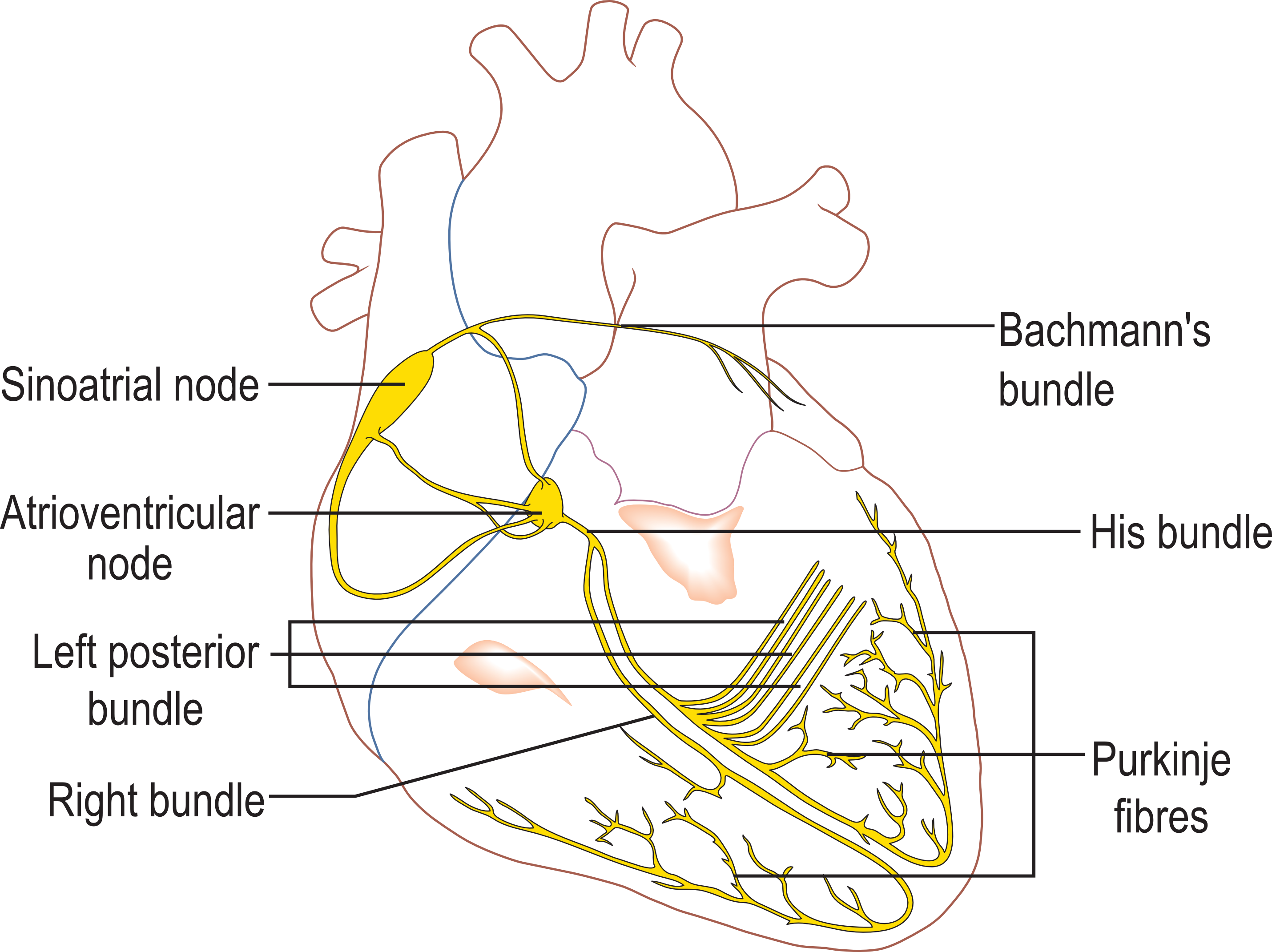
Unlike skeletal muscles, the heart contraction is not triggered by the release of neuro-transmitters in the neuromuscular junction. Under normal conditions, the harmonious, orderly, efficient contraction of the heart is initiated by a group of cells located in the right atrium: the sinus node (SN), sometimes referred to as our natural pacemaker. The role of the nervous system is here indirect: it modulates the activity of autonomous rhythmic heart cells that the sinus node is a part of.
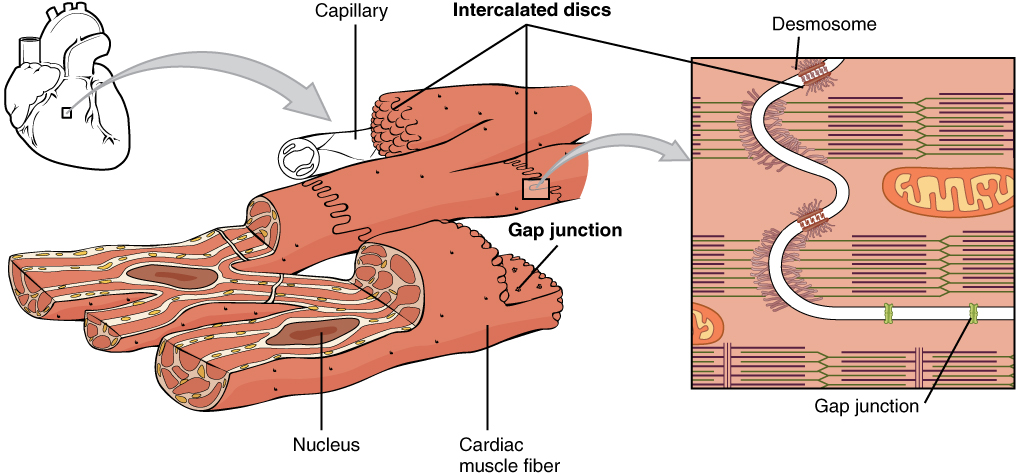
The contraction signal is mediated by a change of transmembrane potential (action potential) in the cardiac cells (the cardiomyocytes). This voltage change propagates throughout the whole heart tissue (the myocardium) via various structures among which the gap junctions, that connect adjacent cells’ cytoplasms to form a syncytium, play a major role.
This propagation is faster in specialised groups of cells that constitute the conduction system of the heart illustrated in fig. 1. It follows preferred directions, guided by the arrangement of myocardial fibres, that reflects the underlying organisation of cells at the histological level. In a physiological setting, this excitation wave, initiated in the SN only, reaches each part of the myocardium only once.
Except in specific affections, the electrical communication between the atria and the ventricles is unidirectional and possible through a unique checkpoint: the atrio-ventricular node. This is why from now on in this manuscript, which focuses on abnormal electrical behaviours of the left ventricle, we will allow ourselves to barely mention the atria anymore, for which modelling has its own specificities and challenges (Dössel et al. 2012). This reductionism obviously comes with limitations, but “what is simple is always wrong; what is not is unusable.”2
1.1.1.3 Cardiac action potential
Because of differences in the concentrations of ions between the cytoplasm and the extra-cellular compartment, there is a measurable difference of electrical potential between the inside and the outside of the double lipidic cellular membrane: the cell resting potential, negative in the human ventricle cardiomyocytes. The AP mentioned in the previous section is a voltage-induced, localised, quick and propagating change of ions concentrations inside and outside the cardiac cell. Altough moderate, this change in concentration transiently reverses the polarity of the transmembrane potential (fig. 3). This change is due to the activation of specialised proteins: the ion channels and transporters. These ionophore proteins are located on the cytoplasmic and sarcoplasmic cell membranes, allowing ions to travel across these membranes either passively under the influence of electro-statical and osmotic forces (ion channels) or actively via energy consumption (ion transporters).
In the human ventricular myocyte, this AP is classically divided in 5 different phases, illustrated schematically in fig. 3. Phase 0 is a rapid depolarisation of the membrane mainly involving the opening of sodium and calcium channels.3 These positive ionic species, which concentration is low in the cytoplasm during the resting potential, quickly raise the transmembrane potential to a positive voltage. Phase 1 is a transient notch before the closing of sodium channels and the characteristic plateau of phase 2, where an inward flux of calcium ions is electrically balanced by an outward flux of potassium ions. The calcium ions, by binding to specific receptors on the protein machinery responsible for the contraction of cardiomyocytes, actually constitute the true messengers of the contraction signal at the sub-cellular level. Finally, phase 3 is the repolarisation phase where after the closing of the calcium channels, potassium channels repolarize the cell to its resting potential (phase 4).
It is important to mention here that the sodium channels involved in phase 0 are voltage-dependent: they only open if the membrane potential is raised above a certain threshold value. This initial raise in voltage is mediated by nearby ionic movements in the same cell or between cells through specific structures (gap junctions). Thus, the influence of a cell’s neighbourhood is what causes the propagation of the AP through the heart tissue.
From phase 1 to phase 3, no change in membrane potential can trigger another depolarisation, creating an absolute refractory period of the cardiomyocyte. The effective refractory period in fact extends to a certain duration during phase 4, where despite a membrane potential equal to the resting potential, no new excitation is possible. This can be seen as a “natural safety mechanism” to prevent constant re-excitation by a single depolarisation wave.
1.1.2 Infarct and arrhythmia
![Figure 4: Infarct. [A] overview of the coronary system; [B] cross-section of the coronary artery with details on the occlusion process. In this thesis, we prefer the term “infarct scar” over “dead heart muscle,” and differenciate various levels of scar/healthy cell combinations throughout the organ. (illustration from https://www.nhlbi.nih.gov/health-topics/heart-attack, public domain)](fig/infarct.png)
The pumping function of the heart is also responsible for transporting oxygen and nutrients to the heart itself via the arterial coronary system. When this process is disturbed by occlusions of vessels in this system (fig. 4), the cardiomyocytes activity is inefficient: this painful process is the acute phase of infarction. If the occlusion lasts, the myocardium suffers irreversible changes (chronic infarction): muscular cells are replaced by fibrotic tissue which contractility and electrochemical properties differ from healthy myocytes.
The past decades have seen dramatic improvements in survival rates of acute infarcts, but the permanent damages of the cardiac muscle are responsible for a large part of infarct-related mortality and morbidity in rich countries. These chronic affections include heart failure when they are related to the pumping function of the heart and arrhythmia when we talk about the pathological effects on the depolarisation wave conduction.
One particular infarct related arrhythmia is the re-entrant ventricular tachycardia (VT). In chronic infarct related VT, instead of “crashing” in the late repolarisation sites of the myocardium, a depolarisation wave re-excites (re-enters) parts of the myocardium that are out of their refractory period. The ventricle thus enters a self-sustained, disorganised, rapid and inefficient contraction of the heart, short-circuiting the physiological role of the SN. In the worst cases this leads to an even more disorganised and lethal arrhythmia: ventricular fibrillation.
1.1.3 VT therapy
Different therapeutic approaches are possible for ischaemic related VT. On one hand, a possible symptomatic treatment of VT relies on the implantation of an implantable cardioverter defibrillator (ICD) that detects arrhythmia and delivers electric shocks (cardioversion) to the patient when needed. On the other hand, the etiologic treatment for VT is the ablation, usually with radio frequencies (RFA), of the arrhythmogenic substrate, i.e., the electrical inactivation of the zones responsible for the re-entry. The details of the risks and challenges of this approach are detailed in the introductions of the articles reproduced in section 2.
During these procedures, the interventional cardiologist first records the electrical activity of the cardiomyocytes. For the work presented in this manuscript, we had access to such recordings for 10 different patients, that helped us build the major part of our scientific contributions.
It is worth mentioning here that cardiac radiology, and particularly computed tomography and magnetic resonance imaging, by providing insights on the topology of the ischaemic scar prior to entering the catheter lab, are very valuable for such interventions (Berruezo et al. 2015).
1.2 Cardiac electrophysiological models
1.2.1 At the cell level
The inspiration for mathematical models of action potential is the Hodgkin–Huxley model (Hodgkin and Huxley 1952) for which the authors were awarded the Nobel prize in 1962. This model aimed at reproducing the electrical behaviour of neurons of giant squids, by extensively describing the movements of ions across their membranes (neurons, like cardiomyocytes, exhibits action potentials when activated). A lot of models in the same spirit have specifically been developed for the description of action potentials of cardiomyocytes, and are regularly updated with new insights from molecular biology.
These cell-level models of cardiac electrophysiology (EP) can be divided in two subgroups:4
“Extensive” models: they incorporate detailed information on the behaviour of numerous ionic channels (Luo C H and Rudy Y 1991), even if they remain computationally tractable for whole organ simulations (Ten Tusscher et al. 2004). They can be specific to certain animal species (Mahajan et al. 2008) or to a cardiac cavity (Courtemanche, Ramirez, and Nattel 1998).
“Simplified” models (Aliev and Panfilov 1996; Mitchell and Schaeffer 2003; Gray and Franz 2020), which aim at reproducing the general changes of voltage over time and specific properties surrounding this change in cardiac cells. These models, which generally group several ionic movements together, follow the philosophy of the FitzHugh-Nagumo model (FitzHugh 1955), that was a phenomenological simplification of the Hodgkin–Huxley model (Hodgkin and Huxley 1952). In this manuscript, we will only use this second type of AP models (section 4).
1.2.2 Reaction-diffusion
In order to move from single cell to organ-level simulations of cardiac electrical activity, these models must be associated to a mathematical description of how the changes in voltage propagate from one “virtual cell”5 to the other.
The most accurate formulation of this behaviour is the bi-domain model. In this model, we consider the extra-cellular and intra-cellular spaces as different compartments separated by the cell membrane. Since the partial differential equations governing the bi-domain model are complex and the numerical schemes required to run simulations with them are computationally expensive, it is common to use a simplification called the mono-domain model. In the mono-domain model, we consider that the intra and extra cellular domains have equal anisotropy ratio. It can be formulated as:
\[\begin{cases} \chi \left( C_m \frac{\partial v}{\partial t} + I_{ion}(v, \eta ) \right) = \nabla \cdot (\sigma \nabla v) \\ \frac{\partial \eta}{\partial t} = f(v, \eta ) \end{cases} \](1)
Here, \(\chi\) is the surface-volume ratio; \(C_m\) the membrane capacitance; \(\sigma\) the conductivity; \(\frac{\partial v}{\partial t}\) the rate of change of \(v\) (the transmembrane potential) with time; \(I_{ion}\) represents the total ion current, a function of \(v\) and a vector of state variables \(\eta\). \(\eta\) represents one of the cell-level models evoked in the previous section and is a function of \(v\) and other variables specific to the chosen ionic model.
This type of model has been successfully used to model re-entrant VT (Lopez-Perez et al. 2019; Relan, Chinchapatnam, et al. 2011). But even in this simplified formulation, its parameterisation is challenging, because most of the parameters are inaccessible to in vivo exploration in human subjects. We will try to address this problematic in section 3 of this thesis.
1.2.3 Eikonal models
Going further down the simplification path, Eikonal models of cardiac electrophysiology form a distinct category, that we investigate in section 2. These categories of models ignore, at least partly, the complexity of the dynamics of voltage changes in the cardiac membrane. They make the assumption that the propagation of the APs in the myocardium can be described as a wave. This makes them a lot easier to parameterise, and extremely fast to compute, at the cost of losing the possibility to simulate complex phenomena although many variants have been proposed to overcome this limitation (Pernod et al. 2011).
1.2.4 Goals of cardiac modelling
There are different reasons why one would want to model cardiac electrical activity.
Models and simulations can help understanding the conditions of a known, experimentally observed phenomenon (Seemann et al. 2006). This approach mostly lies in the category of basic science; for instance, one could wonder which ion channels are responsible for specific changes in phases of the AP, or what conduction speeds are necessary to observe a certain phenomenon at a larger scale.
On the other hand, models can also be used for their predictive power; an approach that is already actively used for drug design (Tomek et al. 2020). The work presented in this manuscript also takes advantage of model predictions, and belongs to the field of patient-specific model personalisation.
1.2.5 Patient-specific models
Adapting model parameters to a specific patient is part of the general field of personalised medicine (Corral-Acero et al. 2020) and can be useful for both prognosis refining and therapy planning (Trayanova, Doshi, and Prakosa 2020).
For pump-function related affections, mechanical models generally have to take into account the circulatory system; yet successes in the personalisation process are found in the scientific literature (Molléro et al. 2018). Concerning EP model personalisation, it can be relevant to consider the isolated heart, because of its (relative) electrical isolation when we consider depolarisation wave propagation dynamics; this is our approach in this thesis.
The electrocardiogram imaging (ECGi) inverse problem can be seen as a model personalisation problem. Its goal is to recover, non-invasively, the activation sequence of the myocardium (similar to the activation maps obtained by interventional cardiologists during RFA procedures) from body surface electrode potentials. Due to the ill-posedness nature of the ECGi problem, priors in the form of EP models have been shown to vastly improve the results, notably when theses models incorporate patient-specific imaging data as part of the personalisation process (Giffard-Roisin, Jackson, et al. 2016).
Our work is related to this approach: we set out to establish a patient-specific EP model personalisation framework, based on patient data acquired non-invasively, usable in the context of ischaemic VT. Unlike previous related studies (Relan, Chinchapatnam, et al. 2011; Relan, Pop, et al. 2011), invasively acquired patient data will not be used directly in the personalisation process, but will allow us to investigate how cardiac computed tomography (CT) features can be translated into EP properties.
1.3 Main contributions
Our main contributions, presented throughout this manuscript are the following:
an image-based Eikonal model personalisation framework using myocardial wall thickness to adjust conduction velocity and able to reproduce periodic activation maps (section 2.1),
a deep learning approach to segment the myocardial wall on high resolution three-dimensional CT images with an accuracy within inter-expert variability (section 2.3.2.1),
signal processing algorithms tailored for the detection of the challenging repolarisation wave on intra-cardiac unipolar electrograms (section 3.2),
a relationship between the thickness of the myocardium and its repolarisation properties (section 3.4.2),
an image-based mono-domain personalisation framework using myocardial wall thickness for personalisation of conduction velocity and restitution (section 4.3).
1.4 Manuscript organisation
In section 2, we present different contributions for Eikonal model personalisation, that also cover image processing algorithms related to the personalisation process and an imaging/electroanatomical maps registration process used to compare simulations and clinical EP data. We then reproduced integral versions of our previously published peer-reviewed publications.
In section 3, we extract repolarisation features from intra-cardiac unipolar electrograms and link these features to the myocardial wall thickness. As is the case throughout this thesis, scar assessment is based on the left ventricle wall thickness on CT images, therefore in the case of chronic myocardial infarction.
Finally, in section 4, making good use of the results obtained in section 3, we focus on a mono-domain model of cardiac EP. We show that the repolarisation features obtained in the previous chapter are able to reproduce arrhythmia induction protocols used by interventional cardiologists in the context of post-infarct VT.
2 Eikonal modelling
Eikonal models usually output activation maps, i.e., local activation times (LAT) associated to coordinates in space; in most Eikonal variants, this map represents only one cycle of activation of the myocardium. Interventional cardiologists are familiar with this type of maps, because based on the hypothesis of activation periodicity, most EP lab terminals reconstruct the activation map of a whole cardiac cavity by aggregating and synchronising data acquired during different cycles. This is necessary because many exploration catheters can only acquire data on a small part of the myocardium at each cycle. During this recording, the clinician needs to move the catheter inside the cavity during numerous consecutive cycles to recreate an activation map of the whole cavity during one cycle. This explains the surprising geometries and in part at least, the presence of seemingly aberrant LATs found in clinical activation maps.
In its simplest form (eq. 2), the Eikonal model only requires a heart geometry, a propagation velocity for each simulation element, and starting point(s) for the depolarisation wave initiation. The simulations are very fast to compute thanks to the fast marching method (Sermesant et al. 2005), making them suited for the development of interactive tools (Pernod et al. 2011) and compatible with clinical time frames (Neic et al. 2017).
Eikonal models of cardiac EP have many limitations for which different solutions have been proposed, for instance to address the anisotropic nature of the AP propagation in the myocardium due to myocardial fibre orientation and/or the front curvature effect (Keener 1991; Jacquemet 2012). Using a multi-front formulation (Pernod et al. 2011; Konukoglu et al. 2011), it is also possible to model more than a single activation cycle.
In this thesis, we mostly used the simplest formulation of the Eikonal model with the exception of our participation in a modelling challenge presented in section 2.4.
In this chapter, we reproduced integral versions of our publications in peer-reviewed conferences (section 2.1, 2.3 and 2.4) and journal (section 2.2). They all concern the Eikonal model of cardiac EP.
Our first publication (VT Scan: Towards an Efficient Pipeline from Computed Tomography Images to Ventricular Tachycardia Ablation, section 2.1) must be seen as a first attempt to use CT imaging as a support for model personalisation in the context of ischaemic re-entrant VT. While we do not introduce any major modification to the formulation of the Eikonal model, we propose direct ways to personalise it based on wall thickness and to reproduce real intra-cardiac recordings of re-entrant VT by imposing a refractory plane to obtain a unidirectional block. By giving a null conduction speed on a plane behind the starting point of the depolarisation and orthogonal to the initial propagation direction, we model the unidirectional propagation pattern typically found in post-infarct VT.
Using this formulation, we present visual results in section 2.1.5 that aims to convince the reader about the pertinence of cardiac CT imaging as a support for patient-specific simulations.
Our contributions in this article are:
a relationship between CT LV wall thickness and depolarisation wave front apparent propagation speed (section 2.1.3.2),
a way to model refractoriness in Eikonal models for unidirectional blocks (section 2.1.3).
In section 2.2, our journal article (Fast Personalised Electrophysiological Models from CT Images for Ventricular Tachycardia Ablation Planning) incorporates the results of the previous conference article, and extends it in various ways.
First, the article reflects the fact that between the two articles we could retrieve more EP data coupled with CT imaging. This allowed to test our personalisation process for activation maps of controlled pacing and not just VT.
Secondly, in an attempt to automate the VT isthmuses detection on CT images, we introduce a channelness filter, purely based on imaging features.
Thirdly, it briefly describes a multi-modal registration framework based on spherical coordinates that eased the comparisons between CT-based simulations and EP data in our work. These spherical coordinates are in the spirit of the universal ventricular coordinates (Bayer et al. 2018) proposed by others during the same year. This framework was also used in comparative studies between different imaging modalities (Nuñez-Garcia, Cedilnik, Jia, Cochet, et al. 2020; Magat et al. 2020) in collaboration with scientists and clinicians from the Bordeaux University.
Our contributions in this article are:
a registration framework for multi-modal data integration (section 2.2.2.7),
an image processing algorithm to identify potential VT isthmuses on CT images (section 2.2.2.6),
a validation of the thickness/speed relationship on controlled pacing electro-anatomical maps (section 2.2.3.3).
Since our goal is to establish a clinically usable model personalisation framework in the short term, and since this framework relies on CT imaging segmentation, it made sense for us to explore automated segmentation strategies in the conference article presented in section 2.3 (Fully Automated Electrophysiological Model Personalisation Framework from CT Imaging). In this section we developed deep learning methods for left ventricular wall segmentation in CT images, with some specific adaptations. Besides the usual segmentations scores (Dice score, Hausdorff distance) used to evaluate this task, knowing that our personalisation methodology relies on LV wall thickness assessment, we evaluated the impact of such image processing approach on this feature. The segmentation network presented in this section was also used in imaging related publications resulting from our collaboration with researchers and clinicians from the Bordeaux Hospital (Nuñez-Garcia, Cedilnik, Jia, Sermesant, et al. 2020; Nuñez-Garcia, Cedilnik, Jia, Cochet, et al. 2020). Unlike the previously proposed model-based approach for this task (Ecabert et al. 2008), our segmentation methodology is purely data-driven.
This article also introduces a way to simulate unipolar electrograms and body surface potentials from activation maps, such as those produced by but not limited to the Eikonal model. Several extensions of the Eikonal model were proposed to simulate ECGs, for instance Pezzuto et al. (2017), here we directly estimate a local dipole and compute the local electrical field using the dipole formulation detailed by Giffard-Roisin, Jackson, et al. (2016). This electrogram rapid simulations framework was also used in a novel formulation of the ECGi inverse problem (Bacoyannis et al. 2019).
Our contributions in this article are:
a deep learning approach to segment the myocardial wall on high resolution three-dimensional CT images (section 2.3.2.1),
an electrogram simulation model formulation by combining the Eikonal model with an ionic model and the dipole formulation (section 2.3.3.4).
In section 2.4 (Eikonal Model Personalisation Using Invasive Data to Predict Cardiac Resynchronisation Therapy Electrophysiological Response), we applied our cardiac EP model personalisation approach to cardiac resynchronisation therapy (CRT) response.
Contrarily to the rest of our work, model personalisation here is based on invasive data. However, this invasive data, intracardiac recordings of electric activity, is of the same nature as the data we used elsewhere as our support for model calibration and validation. Exploitation of such data is not trivial, notably for reasons evoked in this chapter introduction, and working with this EP data helped us apprehend our main research focus with a sharpened eye. More precisely, we here addressed the question of precisely detecting the depolarisation onsets and deriving wave front propagation speed from such data.
We also illustrate in this section some of the possible variations of Eikonal models that we mentioned earlier.
Our contributions in this article are:
a methodology to identify initial depolarisation sites on incomplete intra-cardiac EP data (section 2.4.4),
an Eikonal model-based approach to identify apparent propagation speed on intra-cardiac electro-anatomical maps (section 2.4.2.2).
Cedilnik, N., Duchateau, J., Dubois, R., Jaïs, P., Cochet, H., and Sermesant, M. Functional Imaging and Modelling of the Heartfimh2017
2.1 VT scan
2.1.1 Introduction
Sudden cardiac death (SCD) due to ventricular arrhythmia is responsible for hundreds of thousands of deaths each year (Mozaffarian et al. 2016). A high proportion of these arrhythmias are related to ischemic cardiomyopathy, which promotes both ventricular fibrillation and ventricular tachycardia (VT). The cornerstone of SCD prevention in an individual at risk is the use of an implantable cardioverter defibrillator (ICD). ICDs reduce mortality, but recurrent VT in recipients are a source of important morbidity. VT causes syncope, heart failure, painful shocks and repetitive ICD interventions reducing device lifespan. In a small number of cases called arrhythmic storms, the arrhythmia burden is such that the ICD can be insufficient to avoid arrhythmic death.
In this context, radio-frequency ablation aiming at eliminating re-entry circuits responsible for VT has emerged as an interesting option. VT ablation has already demonstrated its benefits (Ghanbari et al. 2014) but still lacks clinical consensus on optimal ablation strategy (Aliot et al. 2009). Two classical strategies have been developped by electrophysiologists. The first strategy focuses on mapping the arrhythmia circuit by inducing VT before ablating the critical isthmus. The second strategy focuses on the substrate, eliminating all abnormal potentials that may contain such isthmuses.
Both strategies are very time-consuming, with long mapping and ablation phases respectively, and procedures are therefore often incomplete in patients with poor general condition. Many authors have thus shown an interest in developing methods coupling non-invasive exploration and modelling to predict both VT risk and optimal ablation targets (Ashikaga et al. 2013; H. Arevalo et al. 2013; Rocio Cabrera-Lozoya et al. 2014; Chen et al. 2016; Wang et al. 2016). Most of the published work in this area relies on cardiac magnetic resonance imaging (CMR), at the moment considered as the gold standard to assess myocardial scar, in particular using late gadolinium enhancement sequences. However, despite being the reference method to detect fibrosis infiltration in healthy tissue, CMR methods clinically available still lack spatial resolution under 2 mm to accurately assess scar heterogeneity in chronic healed myocardial infarction, because the latter is associated with severe wall thinning (down to 1 mm). Moreover, most patients recruited for VT ablation cannot undergo CMR due to an already implanted ICD.
In contrast, recent advances in cardiac computed tomography (CT) technology now enable the assessment of cardiac anatomy with extremely high spatial resolution. We hypothesized that such resolution could be of value in assessing the heterogeneity of myocardial thickness in chronic healed infarcts. Based on our clinical practice, we indeed believe that detecting VT isthmuses relies on detecting thin residual layers of muscle cells-rich tissue inside infarct scars that CMR fails to identify due to partial volume effect. CT image acquisistion is less operator-dependent than CMR, making it a first class imaging modality for automated and reproductible processing pipelines. CT presents fewer contraindication than CMR (it is notably feasible in patients with ICD), it costs less, and its availability is superior.
The aim of this study was to assess the relationship between wall thickness heterogeneity, as assessed by CT, and ventricular tachycardia mechanisms in chronic myocardial infarction, using a computational approach (see the overall pipeline in fig. 5). This manuscript presents the first steps of this pipeline, in order to evaluate the relationship between simulations based on wall thickness and electro-anatomical mapping data.
2.1.2 Image Acquisition and Processing
2.1.2.1 Population
The data we used come from 7 patients (age 58 \(\pm\) 7 years, 1 woman) referred for catheter ablation therapy in the context of post-infarction ventricular tachycardia. The protocol of this study was approved by the local research ethics committee.
2.1.2.2 Acquisition
All the patients underwent contrast-enhanced ECG-gated cardiac multi-detector CT (MDCT) using a 64-slice clinical scanner (SOMATOM Definition, Siemens Medical Systems, Forchheim, Germany) between 1 to 3 days prior to the electrophysiological study. This imaging study was performed as part of standard care as there is an indication to undergo cardiac MDCT before electrophysiological procedures to rule out intra cardiac thrombi. Coronary angiographic images were acquired during the injection of a 120 ml bolus of iomeprol 400 mg/ml (Bracco, Milan, Italy) at a rate of 4 ml/s. Radiation exposure was typically between 2 and 4 mSv. Images were acquired in supine position, with tube current modulation set to end-diastole. The resulting voxels have a dimension of \(0.4\times{}0.4\times{}1\) mm3.
2.1.2.3 Segmentation
The left ventricular endocardium was automatically segmented using a region-growing algorithm, the thresholds to discriminate between the blood pool and the wall being optimized from a prior analysis of blood and wall densities. The epicardium was segmented using a semi-automated tool based on the interpolation of manually-drawn polygons. All analyses were performed using the MUSIC software (IHU Liryc Bordeaux, Inria Sophia Antipolis, France). An example of the result of such segmentation can be seen in fig. 6.
2.1.2.4 Wall Thickness Computation
In CT-scan images, only the healthy part of the myocardium is visible, hence wall thinning is a good marker of scar localization and abnormal electro-physiological parameters (Komatsu et al. 2013). To accurately compute wall thickness, and to overcome difficulties related to its definition on tri-dimensional images, we chose the Yezzi et al. method (Yezzi and Prince 2003). It is based on solving the Laplace equation with Dirichlet boundary conditions to determine the trajectories along which the thickness will be computed. One advantage of such thickness definition is that it is then defined for every voxel, which is later useful in our model (see section 2.1.3.2). An example of the results can be observed in fig. 7 (left and middle), along with a comparison with the much lower level of detail in scar morphology assessment that is obtained with a voltage map from a sinus rhythm recording.
2.1.3 Cardiac Electrophysiology Modelling
2.1.3.1 Eikonal Model
We chose the Eikonal model for simulating the wave front propagation because of the following reasons:
It requires very few parameters compared with biophysical models, making it more suitable for patient-specific personalization in a clinical setting.
Its output is an activation map directly comparable with the clinical data.
It allows for very fast solving thanks to the fast marching algorithm.
We used the standard Eikonal formulation in this study:
\[v(X)||\nabla T(X)|| = 1\](2)
The sole parameter required besides the myocardial geometry is the wave front propagation speed \(v(X)\) (see section 2.1.3.2). More sophisticated biophysical models allow for more precise results; however, this precision relies on an accurate estimate of the parameters and the necessary data to such ends are not available in clinical practice.
This original approach enabled us to parametrize directly the model on the basis of the thickness computed from the images. Additionally, we generated a unidirectional onset by creating an artificial conduction block. This block was needed to represent the refractoriness of the previously activated tissue that the Eikonal model does not include. An illustration of this phenomenon can be observed in the green box in fig. 8.
2.1.3.2 Wave Front Propagation Speed Estimation
As there is a link between myocardial wall thickness and its viability, it was possible to parameterize our model from the previous wall thickness computation (see section 2.1.2.4). There are basically three different cases:
Healthy myocardium where the wave front propagation speed is normal.
Dense fibrotic scar where the wave front propagation is extremely slow.
Gray zone area where it is somewhere in between.
Instead of arbitrarily choosing a specific speed for the “gray zone,” we exploited the resolution offered by our images to come up with a smooth, continuous estimate of the speed between healthy and scar myocardium. This resulted in the following logistic transfer function:
\[v(X) = \frac{v_{max}}{1 + e^{r(p -t(X))}}\](3)
where \(v_{max}\) is the maximum wave front propagation speed, \(t(X)\) the thickness at voxel \(X\), \(p\) the inflection point of the sigmoidal function, i.e., the thickness at which we reach \(\frac{1}{2}v_{max}\) and \(r\) a dimensionless parameter defining the steepness of the transfer function.
More specifically, we chose the following parameters:
\(v_{max} = 0.6\) m/s, as it is the conduction speed of healthy myocardium,
\(p = 3\) mm, as it was considered the gray zone “center,”
\(r = 2\), in order to obtain virtually null speed in areas where thickness is below 2 mm.
The resulting transfer function can be visualized in fig. 8.
The fibre orientations were not included in our simulations. They might be in our final pipeline, but it is worth noting that we obtained satisfying results without this parameter.
2.1.4 Electrophysiological Data
In order to evaluate the simulation results, we compared them to electro-anatomical mapping data. As part of the clinical management of their arrhythmia, all the patients underwent an electrophysiological procedure using a 3-dimensional electro-anatomical mapping system (Rhythmia, Boston scientific, USA) and a basket catheter (Orion, Boston scientific, USA) dedicated to high-density mapping. During the procedure, ventricular tachycardia was induced using a dedicated programmed stimulation protocol, and the arrhythmia could be mapped at extremely high density (about 10 000 points per map). Patients were then treated by catheter ablation targeting the critical isthmus of the recorded tachycardia, as well as potential other targets identified either by pace mapping or sinus rhythm substrate mapping. These maps were manually registered to the CT images.
2.1.5 Results
Examples results of the simulations and their comparisons to mapping data are presented in fig. 9. In each case, a qualitatively similar re-entry circuit is predicted.
Similar visual results were reached for all the VTs, without any further tuning of the model. However, to reach such results we needed to pick the stimulations points and directions very carefully.
2.1.6 Implementation
All the activation maps acquired during ventricular tachycardia (10 maps of 10 different circuits acquired in 7 patients) were exported to Matlab software (Mathworks, USA).
The simulation was computed directly on the voxel data as the resolution of our images represents highly detailed anatomy, and to avoid arbitrary choices inherent to mesh construction. We then mapped the results to a mesh but for visualization purposes only.
We used a custom Python package for the thickness computation and the SimpleITK (Yaniv et al. 2018) fast marching implementation to solve the Eikonal equation.
The artificial conduction block was created by setting the wave front propagation speed to zero in a parametrically defined disk of 15 mm radius, 2 mm behind the stimulation points, orthogonal to the desired stimulation direction.
From the results of the semi-automatic CT image segmentation, the complete simulation pipeline, with an informal benchmark realized on a i7-5500U CPU at 2.40GHz (using only 1 core), looks as follows:
Compute thickness from masks [43s]
Apply transfer function [0.5s]
Select pacing site and create refractory block [7s]
Solve the Eikonal equation [0.5s]2.1.7 Discussion
This article presents a framework that may be suitable for VT RF ablation targets and prediction of VT risk in daily clinical practice. The results presented here are preliminary but promising, due to the robustness of the image processing, the fast simulation of the model, and the high-resolution of CT scan images. This resolution was crucial in the characterization of the VT isthmuses presented in this study.
The main limitations of the results presented here are the limited sample size and the lack of quantitative evaluation of the simulation results. It is however worth noting that we were able to obtain such results without advanced calibration of the model’s parameters. For the latter, we plan to map the electrophysiological data onto the image-based meshes for more quantitative comparison. However it remains challenging due to the shape differences. Heterogeneity in CT images also induce a bias in thickness computation that may require patient-specific personnalization of the transfer function parameters.
We believe that in order to fully automatize the pipeline, we need not only to determine a ridge detection strategy, but also to overcome some of the simplifications induced by the Eikonal modelling choice and enhance the circuit characterization.
Cedilnik, N., Duchateau, J., Dubois, R., Sacher, F., Jaïs, P., Cochet, H., and Sermesant, M. EP-Europace europace2018
2.2 Going further with VT scan
2.2.1 Background
Personalised, i.e., patient-specific, simulation of the heart electrical behaviour is a dynamic research field (Gray and Pathmanathan 2018). Building such simulation is often a challenge as mathematical models can be computationally costly and clinical data is sparse and noisy. Most of the work in this area relies on extracting fibrosis from late-enhancement cardiac magnetic resonance imaging (MRI) (Lopez-Perez, Sebastian, and Ferrero 2015). In a post-infarct context, this geometry is then classically divided into 3 different zones based on MRI signal processing: the healthy myocardium, the dense scar and a grey zone where fibrosis and remaining functional cardiomyocytes coexist. Grouped together, these three zones represent a three-dimensional domain upon which a set of partial differential equations (PDE) is solved. The model parameters are then chosen differently according to the different zones of the domain to represent the different electrophysiological properties of these tissues. Models typically used are reaction-diffusion models (Chen et al. 2016), where the reaction part mimics cell-level changes in membrane potential and the diffusion part reflects the ability of cardiac action potential to propagate through specialised structures. Adequately parameterising such models is a tedious task; solving takes a lot of computational power and time, making them hard to enter medical practice in a clinically compatible time frame.
Additionally, before the actual simulation computation, the binary masks (outputs from image segmentation) often need to be transformed into another three-dimensional representation, a 3D mesh, more suited to finite elements PDE solvers (Lopez-Perez, Sebastian, and Ferrero 2015). Choosing adequate parameters for the mesh generation step is critical in order to reach reasonable numerical accuracy and computational time. It requires specific expertise rarely available on day-to-day clinical practice.
Some authors have reported realistic intra-cardiac electrograms simulation (Rocío Cabrera-Lozoya et al. 2016), but the output of such models are usually visual simulations of the wave front propagation in the cardiac tissue, i.e. activation maps (Chen et al. 2016). Either way, the goal of such simulations is always to identify abnormal activation patterns linked to fatal arrhythmias. They could improve sudden cardiac death (SCD) risk prediction (H. J. Arevalo et al. 2016), a major challenge in cardiology (Hill et al. 2016).
They can also be used to improve post infarct re-entrant ventricular tachycardia (VT) radio-frequency ablation (RFA) outcome by contributing to the planning phase of the intervention (Rocío Cabrera-Lozoya et al. 2016). In these interventions, the VT is usually induced and mapped (when hemodynamically tolerated) allowing the clinician to identify re-entry isthmus(es) to be ablated. This risky and long target identification phase still drastically limits the wide spread and success rate of such interventions. Moreover, most of these patients already carry an implantable cardioverter-defibrillator (ICD), which makes model personalisation from MRI difficult if not impossible.
It has been reported that cardiac computed tomography (CT) images could be useful for VT RFA (Mahida et al. 2017). CT offers better cost, accessibility, inter-centre and inter-personal reproducibility than MRI. Most notably CTs are not a problem in ICD carriers in whom the image quality and spatial resolution are preserved unlike with MRI. This is important as a majority of scar related VT ablations are conducted in ICD carriers. The better resolution of CT images could also be critical in appreciating scar heterogeneity and thus identifying potential targets.
On CT images, the infarct scar is characterised by an apparent thinning of the myocardial wall (Mahida et al. 2017), which has been shown to correlate with low voltage areas (Ghannam et al. 2018). Some VT re-entry isthmuses are also visible on such images, with a characteristic morphology on myocardial wall thickness maps. It has indeed been recently shown that they appear as a zone of moderate thinning bordered by more intense thinning and joining two areas of normal thickness (Ghannam et al. 2018).
In this paper we propose a novel framework to simulate activation maps from CT images. It uses CT myocardial wall thickness to parameterise a fast organ-level wave front propagation model in a pipeline visually represented in fig. 10.
2.2.2 Methods
2.2.2.1 Cardiac Computed Tomography Images
Images were acquired using a contrast-enhanced ECG-gated cardiac multi-detector CT using a 64-slice clinical scanner (SOMATOM Definition, Siemens Medical Systems, Forchheim, Germany). Coronary angiography images were acquired during the injection of a 120 ml bolus of iomeprol 400 mg/ml (Bracco, Milan, Italy) at a rate of 4 ml/s. Radiation exposure was typically between 2 and 4 mSv. Images were acquired in supine position, with tube current modulation set to end-diastole. The resulting voxels have a dimension of 0.4×0.4×1 mm³, superior to what clinically available MRIs can produce. A resulting short-axis slice can be visualised on fig. 10 (left part).
2.2.2.2 Wall Segmentation
On these images, the left ventricle was segmented as follows.
The endocardial mask was segmented using a region-growing algorithm, the thresholds to discriminate between the blood pool and the wall being optimised from a prior analysis of blood and wall densities.
The epicardial mask was segmented using a semi-automated tool built within the MUSIC software (IHU Liryc Bordeaux, Inria Sophia Antipolis, France): splines were manually drawn on a few slices and interpolated in-between.
The resulting myocardial wall mask (epicardial mask minus the endocardial mask) has around one million voxels.
2.2.2.3 Wall Thickness Estimation
On such images, chronic infarct scars appear as a thinning of the myocardial wall (Mahida et al. 2017). To localise scars, instead of successive dilations of the endocardial masks that were used in other studies (Ghannam et al. 2018), we opted for a fully automated and continuous method (Yezzi and Prince 2003). Estimating the thickness of a structure from 3D medical images is not trivial. The accuracy can be compromised depending on how the two surfaces are described, and how the distance between them is computed. In this work, we chose to rely on a robust method to compute the shortest path between the endocardium and the epicardium, and then integrate the distance along this path. This is based on solving a partial differential equation to compute a thickness value at every voxel of the wall mask (Yezzi and Prince 2003). Example results of such thickness maps are presented on fig. 15.
2.2.2.4 Eikonal Model
Numerous models were proposed in the literature to simulate cardiac action potential dynamics. In order to obtain a fast and robust pipeline, we used the Eikonal model of wave front propagation that directly outputs an activation map. It is very robust to changes in image resolution and it can be computed very efficiently with the fast-marching algorithm.
Model inputs are:
The myocardial wall mask, i.e., the domain of resolution.
For every voxels of this mask, a local conduction velocity.
One or more onset point(s), to initiate propagation.
(Optionally) An artificial unidirectional block, in order to orientate the initial propagation, used to reproduce re-entrant VT patterns.
Let \(v\) be the local conduction velocity, \(T\) the local activation time and \(x\) a voxel of the wall mask, the formal expression of this model is the following:
\[v(x) \parallel \nabla T(x) \parallel = 1\]
To solve this equation we used the fast marching algorithm implementation in the Insight Segmentation and Registration Toolkit (ITK, Kitware, USA). It did not require any meshing step as this implementation directly takes advantage of the regular grid of CT 3D images.
2.2.2.5 Model parameters
Due to a “zig-zag” course of activation in surviving bundles existing in the infarcted tissue, the wave front propagates very slowly and finally exits the scar (De Bakker et al. 1993). We hypothesised that the wave front propagation velocity could be estimated from the wall thickness using a transfer function that would have the following features:
It should reach a plateau, \(v_{\max}\), above physiological wall thicknesses.
It should be virtually null, \(v_{\min}\), below certain thicknesses, where almost no conducting cells remain.
Let \(v\) be the velocity at each voxel \(x\) of the domain, \(W\) the thickness, \(p\) the mid-point between “pure scar” and “healthy” thicknesses and \(r\) a parameter influencing the slope of the transition between \(v_{\min}\) and \(v_{\max}\). We designed the following continuous transfer function from wall thickness to wave front propagation fig. 12:
\[v(x) = \frac{v_{\max} - v_{\min}}{1 + e^{r(p - W(x))}} + v_{\min}\]
The fast-marching solver needs a “stopping value,” i.e., a maximum wave front reaching time. In our experiments, we set it to 500 ms and also assigned this value to non-activated parts of the domain.
In order to model a re-entrant VT pattern, we added an artificial “refractory wall,” as previously described in (Cedilnik et al. 2017). A conduction block orthogonal to the isthmus longitudinal axis was added a few voxels behind the simulation onset point. It allows to model tissue refractoriness while staying in the simple Eikonal model framework, allowing fast computations and keeping the computational cost very low. This is only needed to reproduce VT activation maps, not for activation maps from controlled pacing.
2.2.2.6 Automatic ridge detection
In order to detect VT isthmuses based on image criteria alone, we used the objectness filter (Antiga 2007), implementation of the Insight Toolkit (Kitware, USA). It is a generalisation of the Hessian matrix-based vessel detection method described by Frangi (Frangi et al. 1998). We fed this algorithm with a modified version of the thickness map where only potential isthmuses candidates (Ghannam et al. 2018), i.e., moderately thin zones between 2 and 5 mm thickness, remained. We tuned the filter’s parameter to respect the topological properties known to characterise VT isthmuses on CT images (Ghannam et al. 2018). We named the output maps obtained this way channelness maps.
2.2.2.7 Comparison with recorded activation maps
In order to gain insight on our model relevance and limitations, we compared our simulation to activation maps acquired during RFA interventions. These activation maps were produced by the Rhythmia mapping system (Boston Scientific, USA) using a 64-electrodes Orion Catheter. They were recorded during sinus rhythm, controlled pacing and VT. They come in the form of surface triangular meshes in different reference frames than the corresponding CT images.
In order to compare both visually (qualitatively) and numerically (quantitatively) the outputs of our simulations to the reference data, we took advantage of the correlation between low-voltages zones and CT wall thinning areas (Ghannam et al. 2018) to manually align the two geometries. After fitting an ellipsoid to the point cloud and using the ellipsoid’s centre, we defined each point by spherical coordinates. A visual representation of this registration framework is presented on fig. 13. Finally, it was possible to project the data from the EP studies onto the more accurate geometry extracted from the CT images.
Using the ellipsoid long axis and a manually chosen point on the septum, this method also allows the fast and automated generation of bull’s eye plots.
2.2.3 Results
2.2.3.1 Execution time
The semi-automated segmentation of the left ventricle takes around 10 minutes for an experienced user of the MUSIC software. The thickness computation takes about 1 minute, depending on the number of voxels of the wall mask. The actual simulation takes less than 1 minute. The channelness computation is the longest step, around 2 to 4 minutes. This informal benchmark results were measured on an Intel i7-5500U-powered laptop.
2.2.3.2 Automated ridge detection
On all channelness maps, an expert cardiologist and an expert radiologist visually assessed that ridges corresponding to their critical isthmus definition could be detected using the channelness filter.
2.2.3.3 Simulated activation maps
For most cases, the general activation patterns of the simulations obtained using our framework match the recordings when using velocities and thicknesses thresholds found in the literature. As can be seen on fig. 14, scar late activation is visible both on simulations and on controlled pacing. The characteristic figure of eight activation patterns of re-entrant VT can also be accurately reproduced using our framework, when using a refractory wall to give the propagation an initial direction. Video versions are available as supplementary materials to offer a better appreciation of the similar dynamics of wave front propagation between the simulations and the measurements. This is actually the usual way recorded activation maps are visualised by the interventional cardiologist in order to decide ablation targets.
2.2.4 Discussion
2.2.4.1 Model limitations
We voluntarily opted for the simplest cardiac EP model in order to build a fast pipeline. For instance, most of the related work includes an algorithmic fibre orientation estimation that we did not include. We do not believe that it would improve much the results, as fibre orientation and its influence are still hard to estimate, particularly in infarcted zones.
In contrast, we believe that an important phenomenon that our model does not address is the front curvature impact. A straight wave front is known to propagate faster than a curved wave front, but this is not the case in our simulations. In some cases, this results in fast, unrealistic, “U-turns” of the excitation. This could be improved with extensions of the Eikonal model (Chinchapatnam et al. 2008), or by switching to a reaction-diffusion model parameterised on wall thickness. The main challenge will here be to preserve a clinically compatible framework in terms of parameterisation complexity and required computational time.
2.2.4.2 Velocities
Our model probably simplifies activation patterns inside the VT isthmuses by globally slowing down the propagation in them. A recent animal study (Anter et al. 2016) indeed suggests that the depolarisation slows down when entering and exiting the isthmus but propagates normally in between. The wave front would then be slowed down inside the core of the isthmus. However, we think that our global slowing down in the whole isthmus is a relevant averaging simplification at the organ scale. In the case where our further work would show the pro-eminence of this phenomenon, an option would be to use channelness maps to accordingly change velocities in isthmuses.
2.2.4.3 Thickness thresholds
Based on data from a recent study (Ghannam et al. 2018), we defined global thickness thresholds across all patients to discriminate between healthy and scar zones. Specifically, we set them to below 2 mm for “pure scar” and above 5 mm for healthy myocardium. However, in some VT cases, the wave front propagation crossed scar zones too fast and matching the recording proved more challenging.
We noticed that in those cases, for instance the one shown in fig. 16, the simulation output could be drastically improved by shifting these thresholds to higher values, i.e., by raising the \(p\) parameter of our thickness to velocity transfer function. Using patient-specific thresholds both for thickness maps analysis and model parameterisation could improve the use of CT images in the context of VT RFA. These patient-specific thresholds could possibly be determined by the disease history or image features such as the distribution of thickness for a specific myocardial wall.
2.2.4.4 Parameter optimisation
Using the registration of image and EP data in the common frame of reference described in the Methods section, it was possible to define a metric to quantify differences between simulations and ground truths. Using the mean square difference between these data, we therefore optimised the thickness to velocity transfer function parameters (\(v_{\max}\), \(v_{\min}\), \(p\) and \(r\), see fig. 12, to minimise the discrepancy between simulations and recordings. To this end, we used the covariance matrix-evolution strategy algorithm (Hansen, Müller, and Koumoutsakos 2003), suited for this type of non-convex optimisation problem. While minimising the mean square difference did improve the numerical matching of the simulations to the recording, the overall activation pattern actually was often degraded. This is partly due to noise in the target EP data and to the fact that the mean square difference metric may not be adapted to preserving the activation patterns like the typical figure of eight shape of re-entrant VT. How to define this pattern-aware metric is still an open question. The output of the channelness is also highly depending on setting the right parameters for the objectness mapping, including a channelness threshold. These parameters should be optimised and validated on a larger multi-centric database.
2.2.4.5 Conclusion: a clinically compatible modelling framework
The simulation framework presented in this article may be useful for EP modelling to enter clinical practice. It requires little human interaction and expertise to go from imaging data to EP simulations. It is very fast and would even be faster by developing implementations more suited to such purpose than the generic ones we currently use. The availability and reproducibility offered by CT images and such automation could help personalised cardiac modelling to enter clinical applications.
2.2.5 Additional material
Cedilnik, N., Duchateau, J., Sacher, F., Jaïs, P., Cochet, H., and Sermesant, M. Functional Imaging and Modeling of the Heart fimh2019
2.3 Automating the segmentation process
2.3.1 Introduction
Catheter radiofrequency ablation of the ischemic arrhythmogenic substrate has been shown to be efficient to prevent sudden cardiac deaths . This efficiency can partially be attributed to the integration of information extracted from cardiac imaging data both prior to and during the intervention (Yamashita et al. 2016).
While cardiac magnetic resonance imaging is still widely considered the gold standard for ischemic scar assessment and model personalisation (Prakosa et al. 2018), computed tomography (CT) has recently gained interest in the electrophysiological (EP) community. Cardiac CT is indeed able to locate and evaluate the ischemic scar heterogeneity (Mahida et al. 2017). This is possible by identifying zones of myocardial wall thinning and evaluating the severity of this thinning; this approach is even able to predict abnormal electrical activity (Yamashita et al. 2017; Ghannam et al. 2018). Moreover, CT is less affected than MRI by the presence of a implantable cardioverter de- fibrillator, a device commonly found in patients susceptible to undergo catheter ablation of ventricular tachycardia.
Given these scar characteristics on CT images, it is no surprise that CT has been successfully used as a way to personalise EP models (Cedilnik et al. 2018). However, up until now, this personalisation relies on manual or semi-automated segmentation of the left ventricular (LV) wall, despite the availability of efficient three-dimensional medical image automated segmentation methods (Isensee et al. 2018).
In this paper we evaluate the impact of a deep learning automated segmentation approach on CT ischemic scar assessment and the related model personalisation framework. This framework (fig. 17) takes a cardiac CT image as input. The LV is automatically segmented using a neural network, allowing myocardial thickness to be automatically computed (Yezzi and Prince 2003). After choosing a virtual pacing point, activation maps can be simulated using the Eikonal model. Finally, electrograms can be generated through a novel approach presented in section 2.3.2.4.
2.3.2 Methods
2.3.2.1 Deep Learning Segmentation
The deep learning approach we applied is based on a previously described methodology to segment the left atrium (Jia et al. 2018). It relies on the use of two successive specialised U-nets (Isensee et al. 2018). The first is used to coarsely segment the full original CT image. Its output is used to compute the bounding box of the region of interest. This allows a cropping of the original image for a higher resolution segmentation of the desired structures.
2.3.2.1.1 Database and Training
The network was trained from scratch using a database of 500 cardiac manual segmentations of contrast-enhanced CT images. These segmentations comprise the LV endocardium, the LV epicardium and the right ventricular epicardium. We used 450 cases for training per se and 50 cases for validation with a loss function defined as the opposite of a label-wise Dice score. The model was fitted using an nVidia GeForce 1080 Ti provided by the NEF computing platform.
2.3.2.1.2 “Low Resolution” U-Net
The first network’s input is the original CT image resampled to \(128\times 128 \times 128\) voxels and it outputs 3 ventricular masks: 2 for the left ventricle (epicardium and endocardium), 1 epicardial right ventricle. The training data was augmented twice, by 2 random rotation of the original image along each axis in the \(\left[-\frac{\pi}{8}; \frac{\pi}{8} \right]\) interval.
2.3.2.1.3 “High Resolution” U-Net
The second network was trained using cropped CT images around the LV, with 5 mm margins and resampled to \(144\times144\times144\) voxels. Each original image was augmented 20 times: by random rotations in the \(\left[-\frac{\pi}{7}; \frac{\pi}{7} \right]\) range along each axis, a random shearing in the \([-0.1; 0.1]\) range along each axis and the application of Gaussian blur with a kernel using a random standard deviation picked in the \([0.5; 2]\) range for half of the augmentations. The network outputs are the two left ventricular masks.
2.3.2.1.4 Post-processing
The network’s outputs were thresholded at 0.5. In order to obtain spatially coherent masks, they were filtered to keep only the largest connected component and to forbid overlap between masks. Remaining holes in the masks were filled using the most frequent label in the hole neighbourhood. The masks were finally up-sampled to the original CT image resolution using a nearest neighbour interpolation.
2.3.2.2 Thickness Computation
Smooth and robust LV wall thickness estimation is not trivial, especially in three dimensions. It indeed requires to solve a partial differential equation using the endocardium and epicardum masks (Yezzi and Prince 2003). Such approach, which assign a thickness value to each voxel of the LV wall mask, is particularly adapted for simulations on regular grids; it has been previously used to such ends (Cedilnik et al. 2018).
2.3.2.3 Electrophysiological Model
We used the thickness information to parameterise an Eikonal model previously described in (Cedilnik et al. 2018). Briefly, wall thinning is related to a macroscopic slowing of the activation front, due to a microscopic zig-zag course of activation in the infarcted tissue . A random pacing point was chosen in the healthy tissue, defined by a wall thickness superior to 5 mm, to initiate the propagation. The simulation was stopped at 500 ms.
2.3.2.4 Electrogram Simulation with the Eikonal Model
We propose an efficient way to simulate electrograms with the Eikonal model. It couples the activation map with a transmembrane action potential model and a propagation methodology based on the dipole formulation (Giffard-Roisin, Fovargue, et al. 2016). In this framework, every voxel is a considered a dipole with local current density:
\[\mathbf{j}_{eq} = -\sigma \nabla{v},\](4)
where \(\sigma\) is the local conductivity and
\(\nabla{v}\) is the spatial gradient of the potential \(v\). Using the chain rule, we can rewrite eq. 4 as:
\[\mathbf{j}_{eq} = -\sigma \frac{\partial v}{\partial T} \times \frac{\partial T}{\partial X} = -\sigma \frac{\partial v}{\partial T} \nabla{T},\]
where \(\nabla T\) is the gradient of the activation map (output of the Eikonal model).
To compute \(\frac{\partial v}{\partial T}\), we used a forward Euler scheme to solve the Mitchell-Schaeffer cardiomyocite action potential model (Mitchell and Schaeffer 2003) and stored its time derivative. We matched the activation time obtained with this model to the activation time obtained with the Eikonal model. To simulate bipolar electrograms, we placed two virtual electrodes (distance between them: 0.9 mm) inside the heart cavity and subtracted one signal to the other.
In order to handle the activation map gradient values at the mask boundaries, we ignored the gradient component(s) in the direction(s) flowing out of the mask. We adapted the volume used in the dipole moment computation accordingly (Giffard-Roisin, Fovargue, et al. 2016).
2.3.2.5 Evaluation of the Automated Segmentation Impact
In order to evaluate the automated segmentation impact, we focused on 8 cardiac CT images (and their corresponding manual segmentation) of patients suffering of re-entrant VT. Theses images have been used neither for the automated segmentation training nor its validation. For 6 cases (patients 1-6) the original CT images were available; for the remaining 2 cases, resampled images aligned to the heart short axis were used.
Binary masks were resampled to the original CT image resolution when available, in order to compute a Dice score on the LV wall.
To compare thickness and activation maps, a mid wall mesh was generated from the manual wall segmentation. Maps corresponding to manual and automated segmentation were then projected on this common frame of reference. A point-wise comparison was made possible this way, and median differences were computed.
To compare the electrograms obtained with both segmentation methods, they were compared with a Pearson correlation coefficient \(r\).
2.3.3 Results
2.3.3.1 Segmentation
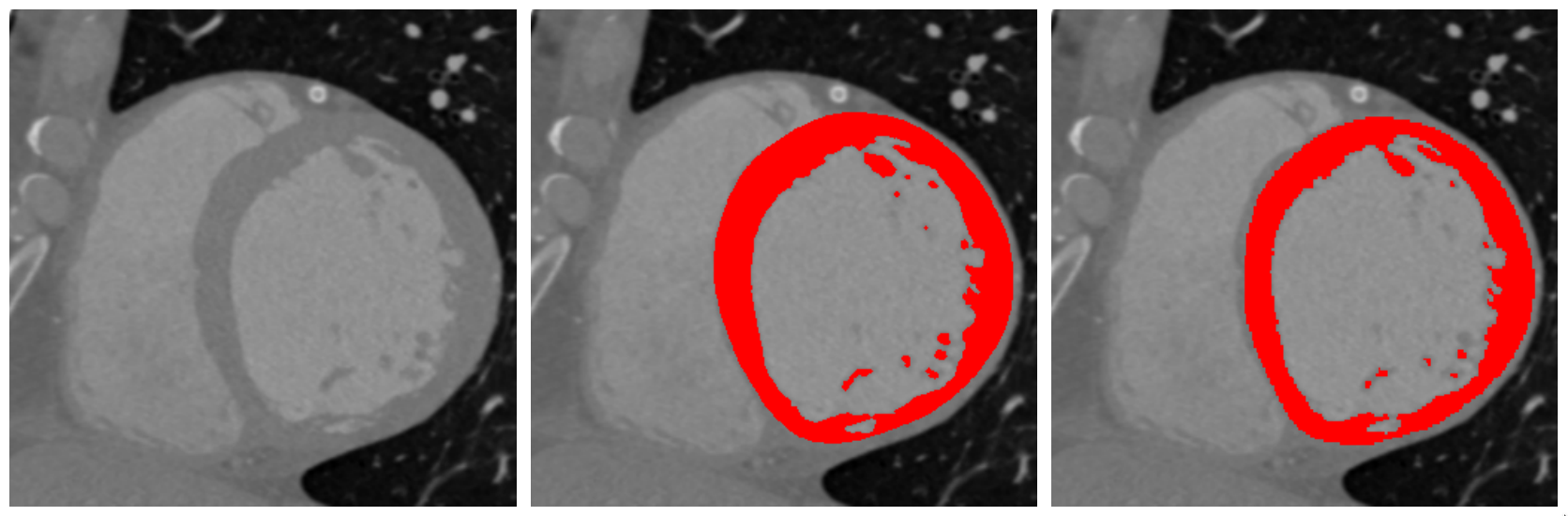
The training phase of the “high resolution” network reached a plateau at a Dice score of \(0.96\) for the LV wall. Data augmentation was key to reaching this high score, especially adding the blur filter.
The median Dice score of the 8 images after up-sampling was lower: \(0.90\). There is no notable difference in the segmentation quality when using original CT images versus short-axis resampled images.
In zones of extreme thinning, the wall continuity was not always observed.
2.3.3.2 Thickness Computation
Across all cases, the median thickness of the manually segmented walls was 5.8 \(\pm\) 3.2 mm versus 5.8 \(\pm\) 3.0 mm for the automatic segmentation. Very sim- ilar thickness maps were obtained using the automated segmentation (median differences across all cases: 0.7 mm, see fig. 19).
2.3.3.3 Eikonal Model
| Patient | DSC | HD (mm) | AHD (mm) | TD (mm) | LATD (ms) | EGr |
|---|---|---|---|---|---|---|
| 1 | 0.88 | 19.15 | 0.10 | 0.7 | 5 | 0.99 |
| 4 | 0.90 | 17.47 | 0.09 | 0.8 | 2 | 0.99 |
| 5 | 0.87 | 13.25 | 0.09 | 0.8 | 3 | 0.99 |
| 6 | 0.91 | 5.00 | 0.05 | 0.5 | 1 | 1.00 |
| 7 | 0.91 | 16.44 | 0.06 | 0.6 | 1 | 1.00 |
| 8 | 0.88 | 7.57 | 0.09 | 1.4 | 29 | 0.75 |
| 9 | 0.89 | 22.86 | 0.11 | 0.7 | 2 | 0.94 |
| 10 | 0.91 | 12.71 | 0.08 | 0.7 | 1 | 0.99 |
| median | 0.90 | 14.85 | 0.09 | 0.7 | 2 | 0.99 |
As expected, given similar thickness maps and geometries, the “virtual pacing” results were very close. The median activation time of the manual segmentation models was \(143\) ms, with a median difference with automated segmentation as little as \(2\) ms across all cases.
2.3.3.4 Electrogram Simulations
Bipolar signals generated with the automated and manual segmentations were virtually identical, with a median Pearson’s \(r\) correlation coefficient of 0.99. All \(r\)s were above 0.94 except one (patient 8, 0.72), and all had \(p\)-values below \(10^{-10}\).
2.3.4 Discussion
2.3.4.1 Segmentation
The automated segmentation algorithm was shown to produce segmentation very close to those obtained by trained radiologists, even with different orientations of the input images. A perfect match between the algorithm and expert segmentation is not desirable anyway as there is also uncertainty in the manual segmentation. The available automated segmentation can probably be improved by training the neural networks on GPUs with more RAM, allowing a better input resolution and less loss of information in the down-sampling phase.
2.3.4.2 Thickness
The differences in the corresponding thickness maps are even smaller. Scar heterogeneity is preserved and comparable between manual and automated segmentation. In some particular cases of wall configuration (holes within the wall…) the thickness computation could be problematic but it only happens in very localised cases which were easy to identify.
Ideally it would have been preferable to compare scar localization on MRI images, but they were not available for these patients.
2.3.4.3 Modelling
As expected, similarity of thickness maps leads to very similar simulation output between the automated and manual segmentation. The wall discontinuities are not problematic at all since they concern zones of extreme wall thinning that are considered non conductive anyway. These explain most of the discrepancy between the resulting activation maps.
2.3.5 Conclusion
We presented in this manuscript the automatic segmentation of the myocardial wall in CT images and the quantification of its impact on personalised models. We showed that most of the infarct related arrhythmia information extraction from CT images are not affected much by using an automated segmentation methodology, proving its robustness. This is another major step towards the future use of EP model personalisation in clinical practice. Furthermore, we presented a novel methodology to generate electrograms from activation maps using the Eikonal model and the dipole formulation. Here we used the same action potential characteristics across the whole domain, but our formulation makes it possible to easily vary them, using the LV wall thickness for instance. Filtering the signals obtained in the same way they are filtered in the EP lab could further improve their realism.
Cedilnik, N., and Sermesant, M. Statistical Atlases and Computational Models of the Heart stacom2019
2.4 Piggy-CRT
2.4.1 Introduction
For our participation in the STACOM piggyCRT challenge, we decided to use the Eikonal model of cardiac electrophysiology (EP). Using the fast marching method, simulations using this model are very fast to solve, which makes them both particularly suited to a clinical workflow (Cedilnik et al. 2018) and easy to personalise. Moreover, as we are only interested in local activation times, the Eikonal model is relevant.
We determined the optimal parameters for this model, i.e., the parameters that minimise the discrepancy between the recorded and the simulated pre-cardiac resynchronisation therapy (CRT) activation maps, for each pig. This model personalisation was then used to predict the post-CRT activation maps using the same parameters (except for the initialisation of the propagation).
2.4.2 Model personalization: general framework
2.4.2.1 Eikonal model
The Eikonal model of cardiac electrophysiology outputs an activation map, i.e., local activation times (LATs) and is defined as follows:
\[v \sqrt{\nabla T^{t} D \nabla T} = 1\](5)
where \(T\) is the local activation time, \(v\) is the local conduction velocity and \(D\) the anisotropic tensor to account for the fibre orientation. We experimented both with fibre orientations generated using the classic Streeter model and the provided OTRBM model.
To make it possible to use multiple onset locations with different delays, we ran one simulation \(T_i\) for each onset \(i\). We then added the desired onset delay \(d_i\) to the whole activation map and combined them into a final activation map by choosing the minimal LAT for each element \(X\) of the domain \(\Omega\):
\[T_{\text{final}} = \min_{\forall X \in \Omega} (T_1(X) + d_1, T_2(X) + d_2, ...)\](6)
Instead of solving the equation on the unstructured grid provided by the challenge, we decided to voxelise them, i.e., to define the domain on a regular lattice of 1 cubic millimetre resolution. Two reasons motivated this choice:
morphological information on an individual heart is generally obtained from the segmentation of imaging data, which is naturally of this form,
the fast marching method is faster on Cartesian grids.
As for the implementation, we used open-source fast marching routines available online (Mirebeau 2017).
2.4.2.2 Parameters fitting with CMA-ES
We used the covariance matrix adaptation - evolution strategy (CMA-ES) (Hansen, Akimoto, and Baudis 2019) genetic algorithm to fit our model parameters to the recorded EP maps. This approach has been used before for a similar challenge (Giffard-Roisin, Fovargue, et al. 2016), and is well suited for multi-parameters, non-convex optimization problems.
We chose to minimise the root median square difference between the recorded data and the simulation output. This choice is justified by the noise on the training data probably due to the acquisition itself and to its registration on the image-derived myocardial geometry. This could lead to outliers driving the root mean square error.
2.4.3 Velocities and domain division

Given this framework, the main parameter that we tried to personalise was the local conduction velocity. But what is the optimal domain decomposition to define the number of local parameters to estimate?
Using different velocities for each voxel would both be impractical (too many parameters to optimise) and does not make sense from a physiological standpoint. Moreover, it would probably result in massive over-fitting to the pre-CRT maps with lower predictive power.
Keeping this in mind, we first tried to optimise a global speed for the whole domain, but also tried by individualising:
both endocardia to capture both the Purkinje network (PN) and the left bundle branch block influences,
both ventricle walls, for the same reason,
the septum, for the same reason and because propagation through the septum could be much slower due to fibre orientation,
the scar if present,
the 17 AHA segments of the left ventricle (LV), to determine if this would be beneficial for the personalisation.
As the optimisation process is reasonably fast with our framework, we decided to test several combinations of these “velocity zones,” as shown in fig. 24.
2.4.4 Onsets
Besides the local propagation velocity, the Eikonal model requires to specify starting points for the wave front propagation. Choosing such points for the pre-CRT sinus rhythm maps is not trivial at all.
2.4.4.1 Locations
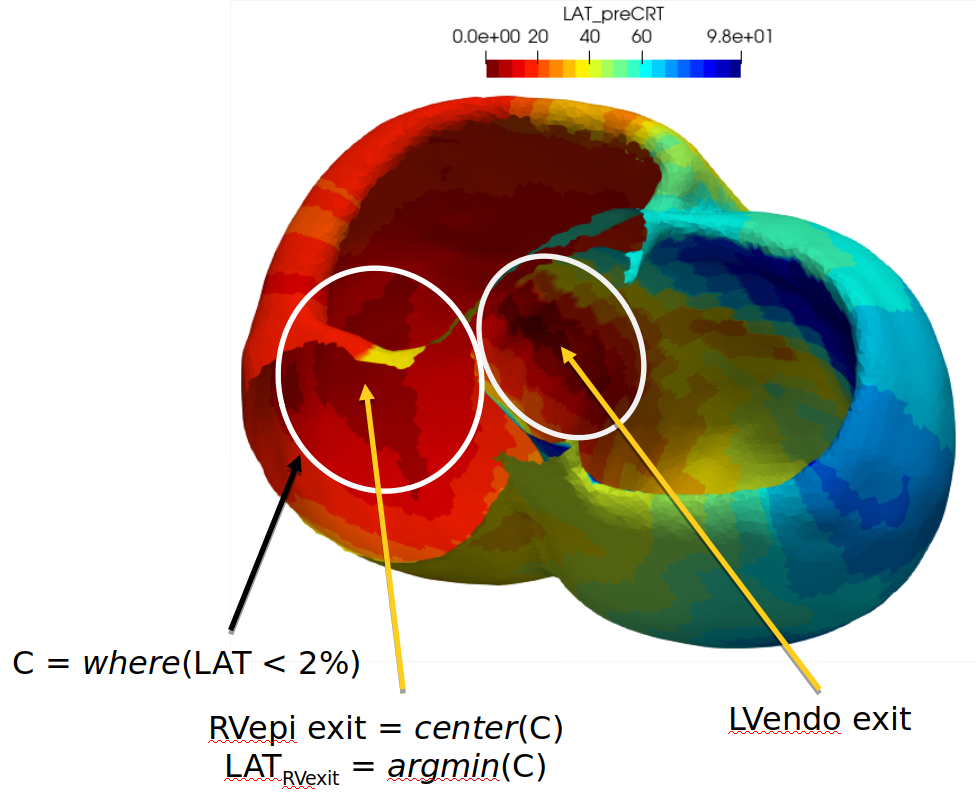
Ideally, the simulated pre-CRT maps should use the atrio-ventricular (AV) node as unique onset. We first tried to parameterise our model in such a way, but this approach rapidly proved very inefficient due to the massive influence of the septomarginal trabecula (ST) in the activation of the right ventricle (RV). As a consequence, it seemed more reasonable to use two different onsets, both in the RV endocardial layer. Unfortunately, the pre-CRT maps did not include any EP study of the RV endocardial surface.
To overcome this limitation of the personalisation data, we chose the centre of gravity of all the points whose pre-CRT LATs were below the second percentile of a given area and picked the closest RV endocardium point. Picking up the point with the smallest LAT may sound more relevant, but because of the propagation spread, likely due to the PN, the simulations fit better using the “percentile” way (more on this in ) This was done for both the LV area, approximately locating the LV onset and the RV area, approximately locating the ST epicardial exit point, as illustrated in fig. 21.
2.4.4.2 Delays
To determine the delays associated to these onsets eq. 6 we proceeded as follows:
Run an Eikonal simulation (eq. 5) for each onset location.
Choose the delay such that the lowest LAT of the simulation match the data, respectively for the LV endocardium (LV onset) and the RV epicardium (ST epicardial breakthrough).
2.4.4.3 Radii
Picking unique points for the onsets caused the optimisation to converge on unrealistically fast velocities to compensate for the spreading of the early activation due to the PN. It seemed logical to overcome this difficulty by “dilating” our onsets. To chose the radius of these dilations, we conducted the following study:
We fixed the endocardial velocity as 3 m/s and scar velocity at 0.1 m/s.
We experimented a wide array of velocities for the rest of the domain, between 0.5 and 4 m/s.
For each velocity, we tested different onset radii, between 0 and 30 mm.
We looked for the optimal myocardial velocity/onset radius combination, i.e., to combination that minimised the median square root error between the EP data and simulations.
The results of this study are shown on fig. 22.
Empirically, we could determine that an onset radius of 10 mm for the pre-CRT simulations and 2 mm for the post-CRT simulations allowed physiology-compatible velocities.
2.4.5 Constraints
We had to define parameter bounds for the optimisation process. We experimented with 3 types of regional constraints:
“Physiological”: \(v_{scar} \in [0, 0.5]\), \(v_{wall} \in [0.5, 1]\), \(v_{endo} \in [1, 4]\)
“Loose”: \(v_{scar} \in [0, 1]\), \(v_{wall} \in [0.5, 2]\), \(v_{endo} \in [1, 6]\), to take into account the fact that the scar might be coarsely located
“No constraints”: \(v \in [0.1, 4]\)
To add a confidence estimation and to evaluate to the relevance of the fibre orientation, the anisotropy ratio, defined as the ratio between the velocity in the transverse plane and the velocity in the fibre direction was also optimised: \(r \in [0.2, 1]\).
2.4.6 Results
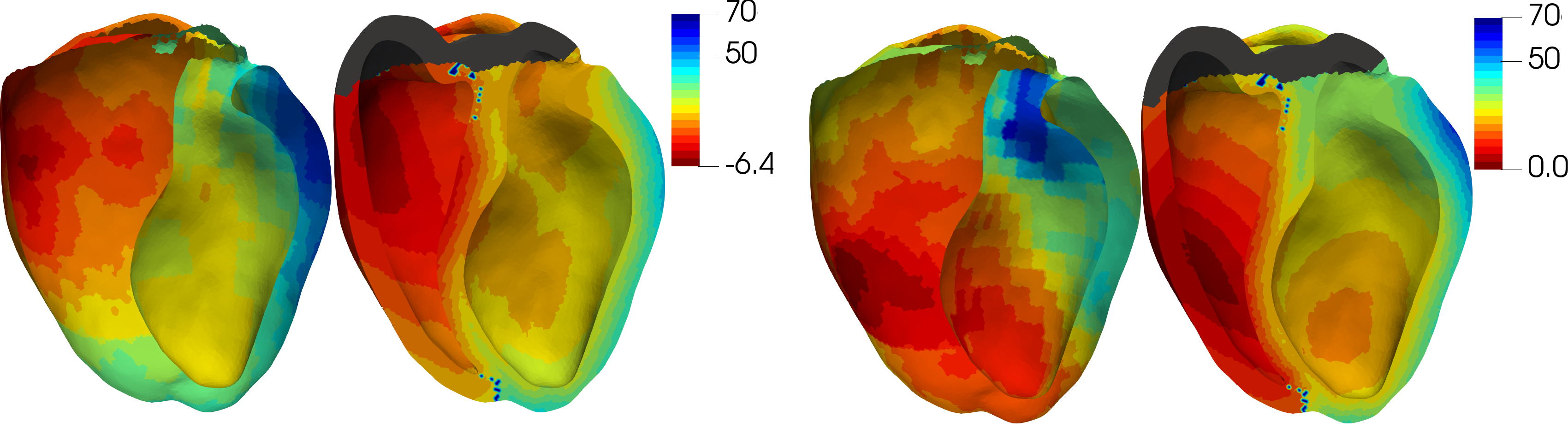
An example of fitting and prediction is shown on fig. 23.
2.4.6.1 Performance
The preCRT fit and CRT response prediction performances of the different constraints and domain divisions are shown in fig. 24 Pre-CRT fit ranged from 9 to 17 ms of median square root difference, while post-CRT prediction performance ranged from 7 to 22 ms.
As expected, a very good preCRT fit is not correlated with a better postCRT prediction, but seems to rather be a sign of over-fitting.
The best approach in terms of prediction performance seems to be using OTRBM fibres and different speeds for both ventricles and both endocardia.
2.4.6.2 Parameters fitting
![Figure 26: Evolution of the parameters values (top) and loss function (bottom) using “loose” constraints for the pig “lali19” during the optimization process. The coloured surfaces represent the [5-95] (light) and [25-75] (darker) percentiles of the parameters (resp. the loss).](fig/stacom2019/cma_loose.png)
Taking a closer look at the optimal parameters, we realised that “physiological” constraints were too strict: best parameters were virtually always 4 m/s for both endocardia and 1 m/s for both walls.
In these conditions, personalisation did not seem to be really interesting and this is what motivated our experiments with “loose” constraints. As can be seen in fig. 25 and 26, this approach made proper personalisation possible.
2.4.7 Discussion
As we were given a very small dataset (3 post-CRT maps) to evaluate the prediction performance, it is really difficult to draw conclusions as to which approach really provides the best personalisation. However it seems clear that dividing the domain in small zones, e.g. the LV AHA segments is both detrimental to the prediction performance and the personalisation duration. We lacked time to explore other parameters combination, for instance, different anisotropy ratios by domain division or even looser constraints.
Our main contribution probably lies in the way we defined the onsets for the pre-CRT simulations and the fast framework proposed. In a clinical setting, personalisation could probably be enhanced with imaging data (Camara et al. 2011; Chen et al. 2016) and possibly ECGI data, and CRT response has to be evaluated with mechanical simulations (Sermesant et al. 2012).
3 Action potential duration in the infarcted human heart
We believe our exploration of the Eikonal models in section 2 makes a strong case for the validity of CT imaging as a personalisation support for ischaemic VT simulations. These very fast-to-compute models, however, lack the ability to effectively simulate the re-entry phenomenon. Besides that, the increase of computational power, notably due to graphics processing units (GPUs), now permits to run mono-domain simulations of cardiac EP in a clinically compatible time frame. This is why we set out to explore such model personalisation based on cardiac CT imaging.
The Eikonal models we presented do not require information about the cardiac action potential variations (section 1.1.1.3), only its apparent propagation velocity (except when used to simulate electrograms in section 2.3.2.4). Reaction-diffusion models, however, must be parameterised with more details to reproduce the behaviour of cardiomyocytes exhibiting an action potential.
One of the main elements of this behaviour is the repolarisation of the cardiac tissue, i.e., the transition between phase 3 and phase 4 (fig. 3) of the cardiac action potential (AP). It corresponds to the process by which the cardiomyocyte cellular membrane goes back to its resting potential, i.e., back to a state where it can be excited again. It is responsible for the absolute refractory period of cardiomyocytes, which is itself linked to the effective refractory period. This phenomenon is of crucial importance for the arrhythmia this PhD manuscript focuses on (Pak et al. 2004). It has been and is still being studied in vitro, in vivo and in silico (Relan 2013; Relan, Chinchapatnam, et al. 2011).
The duration between the start of phase 1 and the end of phase 3 is called the action potential duration (APD). A known property of the heart cells is that the APD is related to the duration between the end of phase 3 of the previous AP and the start of phase 1 of the next AP: the diastolic interval (DI). This is one of the many mechanisms by which the heart adapts to variations in pace, along with changes in its mechanical properties, e.g., its contractility. APD can thus be described as a function of DI to constitute electrical restitution curves (RC, fig. 27), something that was historically described in the the cat (Bass 1975). RCs have an initial steep curve at short DIs before an asymptotic rise to reach a plateau at long DIs. Whether this initial steepness is pro or anti-arrhythmogenic is debated (Franz 2003).
Investigating APDs and RCs directly is very difficult in vivo, but is has been shown that the activation-recovery interval (ARI), or time (ART), observable on unipolar electrograms (UEGs), is a good surrogate of the APD (Xia et al. 2005).
In this chapter, using the data available to us, we investigated the restitution properties of the human heart in terms of APD, in healthy and infarcted areas.
Our main contributions in this chapter are:
an algorithm to determine the start and the end of the depolarisation complex on unipolar electrograms (section 3.2.3),
a methodology to discriminate positive, negative and biphasic depolarisation waves on unipolar electrograms (section 3.2.4.2),
a relationship between CT wall thickness and action potential duration (section 3.4.2).
3.1 Data
We studied 27 EP maps, including sinus rhythms (SR), controlled pacing from the left ventricle (LV), implantable cardioverter-defibrillator (ICD), right ventricle (RV), and ventricular tachycardia (VT) recordings from 7 different patients who underwent radio-frequency ablation of re-entrant VT. All these maps are listed in table 2.
The maps are constituted by a list of 3D coordinates corresponding to a point cloud labelled “Surface Electrodes” by the Rhythmia mapping system. Unipolar, bipolar electrograms and standard 12-lead ECGs were associated with each of these points, sampled at 953.674 kHz.
Each map was manually associated with a global cycle length (CL) ranging from 360 to 1007 milliseconds. This annotation was easy on controlled pacing maps where more than one stimulation artefact was visible on the bipolar trace and on VT maps that all covered more than one cycle length. For SR maps, the global cycle length was determined by using either the bipolar trace, or the 12 lead surface electrode trace after examining the traces for different points until finding one where two depolarisations were visible.
Most maps were recorded in the left ventricular cavity, except for patient #3. For this patient, the maps where epicardial recordings covering parts of both the left and right ventricle.
3.1.1 Inclusions
Some of these maps were already exploited in section 2 but new ones acquired under similar conditions were added, mostly sinus rhythm maps that we did not aim to reproduce with the Eikonal model presented in the previous section.
These maps were registered to CT data using the low-voltage/CT wall thinning relationship (Ghannam et al. 2018). CT thickness information was then projected on EP data using spherical coordinates, symmetrically to what is shown on fig. 13.
3.1.2 Exclusions
Some maps shown in section 2 could not be analysed: they did not include UEGs because of the format they were exported in from the EP console. Two LV paced maps had to be excluded because the stimulation artefacts disturbed the UEGs in a way that made the repolarisation wave detection not doable.
3.2 Activation/recovery time detection
3.2.1 Artefact handling
9 maps presented UEGs where stimulation artefacts were clearly visible and would have disturbed the depolarisation and repolarisation detection. The timings of these artefacts were manually annotated.
Since we would then analyse the derivative of the UEGs, we minimised the impact of these artefacts by linearly interpolating the UEG from 10 samples before to 10 samples after the artefact annotation
An example of (small) artefact can be visualised on the raw UEG trace in fig. 28 and other similar traces in fig. 31.
3.2.2 De-noising filter
Upon manual examination, we estimated that the UEGs were too noisy to be analysed without filtering. After empirical tuning, we found that applying a low-pass Butterworth filter of order 7 at 30 Hz was adapted to our analysis. The filter was applied after the artefact handling described in section 3.2.1.
We used the filtering implementation of the Biosppy6 package which is an easy-to-use wrapper around the SciPy (Virtanen et al. 2020) filtering routines.
This impact of this filter can be visualised in fig. 28 and fig. 31.
3.2.3 Depolarisation detection
3.2.3.1 Depolarisation time
The derivative of the filtered, stimulation artefact-free, UEG was computed using second order accurate central differences, using the gradient implementation of the NumPy package (Harris et al. 2020).
In order to identify the depolarisation wave, we searched for the lowest negative peaks in this derivative (Chen P S et al. 1991) using the find_peaks method of the SciPy package, with a minimum distance of 250 samples. The distance parameter filters out peaks that are closer than the minimum distance based on peak (negative) height. After this filter, we applied a custom peak filtering resulting in the exclusion of peaks with heights inferior than half the height of the highest peak.
We found that this approach allowed to successfully identify depolarisation waves and distinguish them from the repolarisation waves, which are much flatter than depolarisation waves. This is a consequence of phase 0 of AP being much steeper than phase 3.
When two depolarisations were detected, we took the timing of the first one as the depolarisation time. This allowed us to search for the repolarisation wave in a satisfying window.
When three depolarisations were detected, we took the timing of the second one as the depolarisation time. This had the advantage of having both a satisfying repolarisation window and the actual cycle length of the previous depolarisation.
3.2.3.2 Depolarisation complex window
While detecting the depolarisation time was quite robust, it was more complicated to detect the start and the end of the depolarisation complex. Searching for the point where the UEG goes back to zero mV is inefficient for several reasons illustrated on fig. 28 and 31:
the baseline is not always zero,
a lot of UEGs are slightly fragmented either before or after the actual maximum \(\frac{dv}{dt}\) and these bumps should not be considered as part of the repolarisation.
Our idea was then to find the plateau of the UEG, that we defined as the absolute value of derivative being below a certain threshold for a certain number of consecutive samples. Since it was impossible to define such threshold in a homogeneous way for all UEGs, we proposed the following “adaptive plateau finding” algorithm.
Inputs:
v: UEG
lo, hi: minimum and maximum indices for the start of plateau
min_consecutive_samples: minimum number of consecutive samples where absolute derivative has to be below a certain threshold
max_iter: maximum number of iterations where the tolerance is raised
t_i: initial threshold to consider the derivative almost zero
Output: index of the start of plateau
Procedure:
x \(\leftarrow |\frac{dv}{dt}|\)
threshold \(\leftarrow\) initial_threshold
hi_search \(\leftarrow\) hi + min_consecutive_samples
result \(\leftarrow\) -1
iter \(\leftarrow\) 0
for iter from 0 to max_iter do
..n_almost_zeros \(\leftarrow\) 0
..for idx from lo to hi_search do
.…if x[idx] < threshold, then
......n_almost_zeros \(\leftarrow\) n_almost_zeros + 1
......if n_almost_zeros = min_consecutive_samples then
....….return result - min_consecutive_samples
......end if
.…else
....….n_almost_zeros \(\leftarrow\) 0
.…end if
.…threshold \(\leftarrow\) threshold + initial_threshold
..end for
end for
return hi
The start and end of the depolarisation complex were searched from 25 to 200 samples after (respectively before) the depolarisation time, with an initial threshold of 0.005 mV\(\cdot\)sample\(^{-1}\), a minimum consecutive samples of 20 and a maximum number of iterations set to 1000. The maximum number of iterations was reached less than 50 times across all analysed UEGs, making the impact of such UEGs negligible.
The algorithm was implemented in python, sped up with the just-in-time compiler Numba (Lam, Pitrou, and Seibert 2015) in order to make possible the analysis of about 300,000 signals in a reasonable time (less than 1 hour) on a standard desktop computer.
3.2.4 Repolarisation detection
3.2.4.1 Detection window
The repolarisation wave detection window was always set to start as the end of depolarisation complex described in section 3.2.3.2. When more than one depolarisation were visible on the UEG, the end of the window was set at the start of the following depolarisation complex.
When there was only one visible depolarisation, we used the global cycle length of the map to fix the end of the repolarisation wave detection as follows: \(window_{end} = depol_{time} + CL - 100\).
In some cases where the depolarisation was late on the UEG, there was a high probability that the repolarisation wave was not captured. We excluded such UEGs, using the following rule: if \(window_{end}\) was equal to the number of samples and the detection window was narrower than minimum(\(CL/2\), 300 samples).
3.2.4.2 Repolarisation waves polarities
In this detection window, we used the find_peaks function of the SciPy package to search for all positive and negative peaks with a minimum width of 5 samples, and a minimum height of 0, see for fig. 29 for an example. The minimum height parameter filters out peaks that are only relatively positive (respectively negative) to their surroundings and only allows peaks where the UEG is actually positive (respectively negative). The minimum width parameter was used to avoid over-detection of high frequency bumps that slipped through the filtering process.
Peaks that were closer than 25 samples from the detection window were excluded. The area under curve (AUC) of each of these peaks were computed from the left bases to the right bases of the peaks.7 Only the positive parts of the UEG were used for the AUC calculation for positive peaks and reciprocally for negative peaks, making the AUC computation window sometimes actually narrower than the window defined by the left and right bases of a peak.
The peak filtering described above is mostly relative, resulting in a lot of cases where both a positive and a negative repolarisation waves were detected. In consequence, since most of these detections did not reflect a real biphasic repolarisation wave, we discriminated actual biphasic repolarisation waves from bogus detections using the following procedure:
We computed the number of peaks between the two peaks, by finding the number of zero-crossings with hysteresis (with a tolerance of 0.001 mV\(\cdot\)samples\(^ {-1}\)) of the derivative of the UEG between the two peaks. In case this number was above 1, this was the sign of a wandering signal in the repolarisation window and the UEG was excluded.
If there were no peaks between the positive and the negative peak, and one had an AUC more than 3 times the AUC of the other one, the peak with the smallest AUC was excluded. These repolarisation waves are annotated “Auc” in fig. 30.
If none of these criteria were met, but the positive peak preceded the negative peak, the peak with the smallest AUC was exluded, because to our knowledge, such “reverse biphasic peaks” have not been described anywhere in the literature. Such peaks are marked as “Bi” in fig. 30.
After fusion of the repolarisation waves on the left part of fig. 30, we can see on the right part that the positive repolarisation waves correspond to the early repolarisation sites, and the negative repolarisation waves to the late repolarisation sites, in agreement with what is found in the litterature (Relan, Chinchapatnam, et al. 2011; Potse et al. 2009). It is worth noting that the median ARI of biphasic waves is between positive and negative wave. We believe this should be interpreted as an argument to validate our methodology (section 3.2.4.2) to distinguish actual biphasic waves from bogus detections.
3.2.4.3 Repolarisation time
There are two main approaches to detect the repolarisation time. The Wyatt (Wyatt et al. 1981) method was the first to be proposed and relies on taking the maximum \(\frac{dv}{dt}\) for all three types of repolarisation waves. An “alternative method” (Chen P S et al. 1991) that treats repolarisation waves differently based on their polarities was then proposed. However, the recent consensus seems to be that the Wyatt method is the most accurate to detect the repolarisation time (Orini Michele et al. 2019).
To implement this detection, we searched for the highest value of the derivative of the UEG computed as described in section 3.2.3.1. The window of this detection was set between the left base (see section 3.2.4.2) of the peak and the peak itself for positive repolarisation waves, between the peak and its right base for the negative repolarisation waves, and between the negative and positive peaks for biphasic repolarisation waves.
A special case had to be created for bogus detections of negative T waves in rapid rhythms. In case the repolarisation time was less than 25 samples before the end of the detection window, the UEG was annotated as “TOO_CLOSE” (fig. 31) and was excluded.
Finally, ARIs below 100 ms and above 500 ms were considered bogus detections and were excluded.
3.3 Analysis
3.3.1 Per maps
3.3.1.1 Detection quality
| Patient | Rhythm | n ARI | Median ARI (ms) | CL (ms) | %na |
|---|---|---|---|---|---|
| 1 | sinusal | 4662 | 242 | 600 | 0.52 |
| rv paced | 6336 | 245 | 600 | 0.1 | |
| sinusal | 2797 | 316 | 860 | 0.26 | |
| vt | 7790 | 213 | 504 | 0.26 | |
| 2 | sinusal | 1921 | 384 | 930 | 0.38 |
| vt | 3417 | 228 | 453 | 0.59 | |
| 3 | vt | 34173 | 172 | 410 | 0.35 |
| sinusal | 37029 | 302 | 911 | 0.15 | |
| 4 | sinusal | 7281 | 273 | 1007 | 0.22 |
| rv paced | 2939 | 222 | 600 | 0.2 | |
| vt | 1600 | 245 | 534 | 0.23 | |
| vt | 183 | 210 | 548 | 0.2 | |
| sinusal | 1398 | 266 | 650 | 0.61 | |
| 6 | sinusal | 9290 | 303 | 700 | 0.31 |
| rv paced | 8885 | 281 | 600 | 0.21 | |
| vt | 246 | 152 | 386 | 0.75 | |
| 7 | vt | 17640 | 269 | 570 | 0.27 |
| sinusal | 4754 | 225 | 600 | 0.46 | |
| vt | 2328 | 178 | 360 | 0.92 | |
| 8 | sinusal | 3977 | 267 | 720 | 0.41 |
| vt | 858 | 222 | 452 | 0.51 | |
| icd paced | 4873 | 258 | 754 | 0.1 | |
| vt | 4430 | 219 | 442 | 0.35 | |
| 9 | cs paced | 5668 | 222 | 597 | 0.32 |
| vt | 7930 | 207 | 527 | 0.15 | |
| rv paced | 5584 | 241 | 536 | 0.13 | |
| lv paced | 7807 | 213 | 600 | 0.14 |
As can be seen in table 2, detecting valid ARIs was very challenging for rapid ventricular rhythms, and many UEGs ended up being excluded for such maps. This is explained by the very short window in which the repolarisation waves were searched. This can be attributed to two phenomena illustrated in fig. 31
Quite often a positive repolarisation wave is indistinguishable from the positive part of the depolarisation complex, making the repolarisation wave very hard (or impossible) to identify.
A very late negative pseudo repolarisation wave is almost always detected. It is very unlikely that this is the actual repolarisation wave of the underlying tissue, and most likely an influence of the far field and or the beginning of the next depolarisation complex. This is what motivated the special case “TOO_CLOSE” described in section 3.2.4.3.
The other type of challenging maps are the sinus rhythm maps. We attribute the number of UEG exclusions in this type of slow maps to the fact that despite their long cycle length, the UEG recording window was often centred on the depolarisation and the repolarisation wave could not always be seen.
3.3.1.2 Median ARIs
Median values of ARIs for each map are presented both in table 2 and fig. 32.
Despite a probably high number of false detections, there seems to be a quite visible relationship between the cycle length and the median ARI detected in each map. We believe this is an argument for the validity of our detection methodology.
3.3.2 APD restitution variations with CT wall thickness
3.3.2.1 Regression strategies
After the automated detection process, we ended up with nearly 200,000 couples (CLs, ARIs). This raw point cloud can be visualised on the top row of fig. 34.
Our goal was to determine whether there are differences between healthy and scarred myocardium in terms of APDs, but also in terms of response to changes in cycle length. We explored this relationship using 3 different formulations.
First, we fitted eq. 7 to the point cloud corresponding to each level of LV wall CT thinning using a least squares regression approach.
\[APD = a\cdot{}\left(1 - b\cdot{}e^{\frac{-CL}{c}}\right)\](7)
Second, as others have proposed in similar studies (Pop et al. 2012), we also tried fitting a linear function, also by a least squares approach, to the relationship between the inverse of the cycle length and the inverse of the APD.
Since the APD restitution curve is classically established between the previous diastolic interval (DI) and not the cycle length itself, we could numerically switch to APD as a function of DI using the two regressions described above, and the fact that \(APD = DI + CL\). This is presented on the right part of fig. 34, and also in transparency on the bottom row.
Finally, and partly because our final goal was to use this data to parameterise a reaction-diffusion model, we tried fitting the restitution curve analytical formula (eq. 8) of the Mitchell-Schaeffer model (Mitchell and Schaeffer 2003) directly, as other similar studies had done previously (Relan 2013).
\[APD = \tau{}_{close}ln\left(\frac{1 - (1 - h_{min})e^{\frac{-DI}{\tau{}_{open}}}}{h_{min}}\right)\](8)
In this case, the relation has to be established as a function of DI directly. Because of the nature of our data, as others have already noted (Relan, Chinchapatnam, et al. 2011), a least squares approach is not suited for this task, because the measurement errors concerns both the independent and the dependent variables. This can be clearly visualised on the bottom row of fig. 34, where residuals do not appear parallel to the Y axis.
However, an orthogonal least squares or similar approaches are not relevant here either, because the measurements errors are distributed along straight lines with the same negative slope. With this in mind, we designed a custom objective function, defined as the distance between data points and the curve to fit along a straight line of slope -45° (see fig. 33 for an illustration).
This objective function could be minimised using the covariance matrix adaptation-evolution strategy (Hansen, Akimoto, and Baudis 2019).
In eq. 8, both \(h_{min}\) and \(\tau_{open}\) have an impact on the slope of the restitution curve. Since \(\tau_{open}\) also has an influence of the difference between absolute and effective refractory periods and we did not have access to such information, we decided to fix it at the value of 250 ms. We then used relatively loose bounds for both \(h_{min}\) (0.1 to 0.5) and \(\tau_{close}\) (100 to 1000) and let the optimisation process converge.
3.3.2.2 Results
Different regression strategies yield different restitution curves but a few tendencies are conserved across the different formulations (fig. 34). On one hand, APDs appear similar or slightly shorter in moderate thinning (3-5 mm) areas to those found in healthy tissue, roughly the equivalent of the grey zone of MRI-based patient specific simulations. On the other hand, APDs are longer in thinner areas (below 3 mm), and an inverse relationship exists between the severity of thinning and the APD.
3.4 Discussion
To our knowledge, based on the number of UEGs analysed, the results presented in this chapter represent the largest study of this type using in vivo human data. This is also the first time restitution properties are correlated to myocardial wall thickness. The APD values should make a good basis for APD in the human left ventricle that could prove useful for modelling personalisation. It is hard to take a stand on whether the shortening in moderate thinning areas is significant, since this phenomenon is usually observed during acute infarction (Shaw and Rudy 1997).
3.4.1 APD estimation
There are however limitations in our ARI detection process.
Since there is no consensus on best approach for this type of task, we had to build our own detection algorithms. Improvements are most definitely possible in this regard, especially for the very challenging repolarisation wave in rapid rhythms. A possible option might be to use machine learning methods that have been shown to be efficient to segment 12 lead ECGs (Jimenez-Perez, Alcaine, and Camara 2019). This would however require manually annotating a consequent number of UEGs to constitute training, testing and validation datasets.
Besides algorithmic issues, a number of factors are also known to influence APD, and were not taken into account here. First, since our data has been collected on patients undergoing RFA of ischaemic VT, most were probably using medications that alter APD as part of their daily cardiac therapeutic. It may prove valuable to confront patient medication to their APDs. That said, including this relationship would probably require a higher number of patients taking various medications. Moreover, since our end goal here is to personalise models for a comparable population, this might not be crucial.
Finally, APDs are shorter in the epicardial than in the endocardial cells, although Anyukhovsky Evgeny P., Sosunov Eugene A., and Rosen Michael R. (1996) could not find this difference in an in vivo canine study. In spite of this, we decided to analyse endocardial and epicardial recordings together, because (a) we only had epicardial maps for one patient, making it impossible to average interpersonal variations in APDs for the epicardial layer and (b) excluding the patient was an option, but would have considerably diminished the number of UEGs analysed, since the epicardial maps included a lot of points (see patient #3 on table 2). We plan on interacting with our clinical collaborators to gather more recordings, and wish to investigate whether endo/epicardial differences in APD could be shown with our UEG analysis methodology.
Nonetheless, given the large number of maps, patients and UEGs analysed, we believe that the APD information we extracted from the EP maps remains valuable.
3.4.2 APD by wall thickness
As others have argued (Orini et al. 2015; Franz 2003), there is no perfect, unequivocal mathematical formulation to build APD - RC curves from experimental data. This is why we chose to present three different fitting strategies, guided both by what is found in the literature and our goal to use this data to create the model personalisation framework detailed in the next chapter.
An issue we faced while fitting these curves was that we do not have access to the real DI but we rather deduce it from the CL, assuming that both the duration of the previous AP and the duration of the previous CL are equal to those of the considered AP. In a few cases, e.g., rapid maps, where 3 depolarisations are visible, accessing the real DI is possible but we chose to stick to a coherent formulation of the DI-APD relationship across all maps and did use the real DI there either. Ideally, we would like to run our analysis again on UEGs recordings covering a much longer window, allowing to assess APD and the “real” previous DI for all cases and removing the need for the custom fitting strategy described in section 3.3.2.1 and visible on the last row of fig. 34.
The last problem we need to mention in this section concerns registration uncertainties between EP and CT data. Notwithstanding these limitations, given the number of UEGs studies, and coherent results with different regression strategies, we believe our conclusions concerning APDs in moderate thinning areas versus APDs in dense scars are valid.
Our findings concerning longer APDs in dense scar areas is different from the porcine study by Pop et al. (2012) using MR and optical fluorescence imaging to assess APDs. However, (a) it is possible that there are differences between human and porcine myocardiums and (b) the porcine study was conducted shortly (weeks) after the acute infarct episode when our study focus on chronic (several years) infarcts. Longer APDs in scar are compatible with the main idea behind clinical VT induction protocols (illustrated in fig. 42) and our simulations of these protocols, as we will show in the next chapter.
4 Reaction-diffusion modelling
After having gathered information on the repolarisation properties of cardiac tissue, and more importantly on the differences between healthy and scarred myocardium, our next task was to use it to parameterise a reaction-diffusion model.
This chapter will present the cell-level model we chose (section 4.1), the numerical scheme best suited to our personalisation data (section 4.2) and the results of our “virtual EP lab” experiments (section 4.3).
Our main contributions in this chapter are:
an ionic model personalisation framework based on CT imaging (section 4.1.2),
an efficient implementation of the Lattice Boltzmann Method for cardiac EP leveraging the computational power of graphical processing units without needing to resort to low-level programming languages (section 2.1.6),
an in silico version of arrhythmia induction protocols that interventional cardiologists use during radio-frequency ablations (section 4.3).
4.1 Ionic model
4.1.1 Presentation
The Mitchell-Schaeffer model of cardiac action potential (AP) (Mitchell and Schaeffer 2003) has been used in previous studies (Relan, Chinchapatnam, et al. 2011) to model re-entrant ventricular tachycardia (VT). It belongs to the category of simplified ionic models of AP (section 1.2.1), regrouping fluxes of different ionic species together, depending on their effect on the transmembrane potential. Instead of representing the cell membrane permeability to the different ions involved, its limited parameters are related to the general shape of the cardiac AP. This makes it a convenient candidate for our use-case, since (a) the computations involved to obtain solutions are not demanding (b) it does not seem reasonable to expect model personalisation at the ion channel level in the foreseeable future.
In order to explore the impact of its different parameters and help us determine which ones were relevant we developed an interactive tool that can be used in a web browser.8
In this model, two state variables are used:
\(v\) represents the scaled transmembrane potential,
\(h\) acts as a gating variable: it controls the recovery of the virtual cardiac cell, by modulating its excitability and general response to an external current.
The variation of \(v\) over time is given by the following ordinary differential equation:
\[\frac{dv}{dt} = J_{in}(v, h) + J_{out}(v) + J_{stim}\](9)
\(J_{out}\) represents the ionic movements that tend to repolarise the cardiomyocyte membrane.
\[J_{out}(v) = - \frac{v}{\tau_{out}}\](10)
It is governed by the parameter \(\tau_{out}\) that will impact mostly the slope of the phase 3 of the AP.
\(J_{in}\) represents the ionic movements that tend to depolarise the membrane. We used a modified version of \(J_{in}\) that introduces the \(\lambda\) excitability parameter (Djabella, Landau, and Sorine 2007).
\[J_{in}(v, h) = \frac{h(v(v-\lambda)(1 - v))}{\tau_{in}}\](11)
It is governed by \(\tau_{in}\), which will impact the slope of the depolarisation (phase 0). It is also under the dependence of the gating variable \(h\) to mimic the threshold behaviour of excitable cells:
\[\frac{dh}{dt} = \begin{cases} \frac{1 - v}{\tau_{open}} & \text{if}\ v < v_{gate} \\ \frac{v}{\tau_{close}} & \text{if}\ v > v_{gate} \end{cases} \](12)
Given proper parameterisation, this model can exhibit a plateau behaviour (phase 2) and also APD restitution properties similar to what is observed in vivo, see fig. 35 for an example.
Because this framework does not model the autonomic behaviour of cardiac cells and despite the name of the article initially describing this model (a two-current model…), a third current actually has to be involved for the model’s \(v\) variable to exhibit an AP-like behaviour: \(J_{stim}\). This last term represents the external stimulation current that has to be applied in order to initiate the depolarisation (phase 0) by bringing \(v\) above \(v_{gate}\). On our case, \(J_{stim}\) will be the pacing stimulation we apply on a specific location to mimic the stimulation catheter of the interventional cardiologist. In the other locations that we do not stimulate directly, \(v\) might be raised above \(v_{gate}\) by the influence of the propagation (diffusion) of the depolarisation wave from the neighbouring cells, something possible in vivo through specific structures, e.g., gap junctions.
4.1.2 Parameterisation
Our global strategy to parameterise the ionic model is to exploit the conclusions of section 3.
4.1.2.1 The \(\tau_{in}\) time constant and the excitability parameter
As explained in section 4.1, the \(\tau_{in}\) parameter controls the velocity of the inward current that tends to depolarise and thus participate in the steepness of the phase 0 slope of the AP. As animal studies (Dun et al. 2004), reviews (Decker and Rudy 2010), and modelling studies (Rocío Cabrera-Lozoya et al. 2016) have shown that infarcted zones present a relatively flatter phase 0 when compared to healthy myocardium, it made sense to increase this parameter in the infarcted zone. We made the hypothesis that the steepness of phase 0 follows an inverse relationship with the CT thickness, and interpolated values evenly spaced on a logaritmic scale ranging from 3 in the thinnest areas to 0.3, the value used in the original paper (Mitchell and Schaeffer 2003) in the healthy areas (5 mm and above).
Scar areas are expected to be less easily excitable because of the fibrotic tissue. We thus set the lambda parameter from values ranging from 0.3 in the most dense scar areas to 0.01 in the healthy tissue, evenly spaced on a logaritmic scale as shown on fig. 36.
Both \(\tau_{in}\) and \(\lambda\) influence the minimal \(J_{stim}\) value (or similarly the diffusion-related incoming \(v\)) needed to initiate an AP (see fig. 35), thus increasing them participates in the source-sink mismatch effect. Since this effect has been shown to be relevant (Ciaccio et al. 2018) in re-entrant VT, this is another argument for higher values in infarcted areas.
By a similar mechanism, higher \(\tau_{in}\) and \(\lambda\) values reduce the apparent propagation speed of the depolarisation wave. As we have shown in section 2, slower propagation speeds in scarred areas, in relation with the severity of the thinning are a key element to reproduce intra-cardiac recordings (activation maps) of re-entrant VT (fig. 9) and controlled pacing (fig. 15). This is another motivation for the values we chose.
The apex and base of the left ventricle are physiologically thinner than the rest of the myocardium. To account for this, \(\lambda\) was lowered in these zones using the local LV coordinates system described in section 2.2.2.7 as follows. A centrality \(C\) value was computed for each point of the left ventricle using \(C = 2(0.5 - (\phi - 1.5)^2)\) and \(\lambda\) was multiplied by \(1 + C\); \(\lambda\) was then clipped so that no values were below 0 or above 0.5.
4.1.2.2 Other time constants (\(\tau_{open}\), \(\tau_{close}\) and \(\tau_{out}\))
By acting on the rate of recovery of the gating variable \(h\) (see fig. 35), the \(\tau_{open}\) parameter has a major influence on the dissociation between absolute and effective refractory periods of virtual cardiomyocytes. While heterogeneity in these differences may be interesting to simulate arrhythmias, we did not have any argument (or data) to adjust it based on the CT thickness, so we decided to use the same value for \(\tau_{open}\) across the whole domain, as was already mentioned in section 3.3.2.1. Since \(\tau_{open}\) also has an influence on APD restitution curves (RC) (eq. 8), we settled on the value 120 that was compatible with RCs constructed in fig. 34.
The \(\tau_{out}\) parameter was set to be 10 times bigger than the \(\tau_{in}\) parameter, in order to maintain the \(\tau_{in}/\tau_{out}\) constant and limit differences in the steepnesses of the RCs.
Using the following relationship (Mitchell and Schaeffer 2003):
\[APD_{max} = \frac{\tau_{close}}{ log( \frac{\tau_{out}}{4\tau_{in}} ) } \](13)
we chose \(\tau_{close}\) such that \(APD_{max}\) values were compatible with the findings of section 3.
However, since eq. 8 only describes the approximate RC of the Mitchell-Schaeffer model, since eq. 13 does not take into account the influence of \(\lambda\) and since single cell computations of this model are very fast to compute using a forward Euler scheme, we decided to use the results shown in fig. 34 to match the actual observed APD when numerically solving eq. 9 and eq. 12. To do so, we constructed “numerical restitution curves” by applying \(J_{stim}\) with different intervals and numerically observing the time during which \(v\) was above 0.01. Because eq. 13 is less and less valid as \(\lambda\) increases, the “pseudo-\(APD_{max}\)” values retained were 850, 350, 300, 250 and 200 from 0 to 5 mm of thickness.
For the thicknesses that lie in between the bounds we chose in section 3, we linearly interpolated the parameters, and verified that this did not induce unwanted “jumps” in the morphology of RCs for intermediate values. The numerical RCs for these intermediary thicknesses are shown on fig. 36.
4.2 The lattice Boltzmann method
The Lattice Boltzmann Method (LBM) was initially proposed as a numerical scheme to simulate the behaviour of fluids using the Navier-Stokes equations. However, it can also be used for reaction-diffusion simulations as an alternative to the widely used finite elements method. It has been shown to be efficient for cardiac electrical behaviour, using the Mitchell-Schaeffer model (Rapaka et al. 2012) or the Luo-Rudy (Luo C H and Rudy Y 1991) model (Campos et al. 2016).
4.2.1 Formulation
In the LBM framework, the spatial domain is discretised as a regular grid, which makes it particularly suited to deal with segmentations of imaging data which are by nature available in this very format. In order to use the LBM, one has to decide a neighbouring scheme that will determine the number \(m\) of directions in which the diffused species will be able to flow. In our case, and as other have done before (Rapaka et al. 2012; Campos et al. 2016), we chose to let the diffused species flow in 6 directions around each element of the grid, that we will refer to as voxels from now on. These 6 directions are the 6 faces of the cuboid a voxel represents. In the LBM framework, this type of direction discretisation is referred to as \(D_3Q_7\), 3 standing for the 3 dimensions of our domain, and 7 for the number of directions we let \(v\) flow to, because a last “direction” is added to the 6 other ones in order to represent the quantity that stays in place.
Each voxel \(x\) is associated with a particle distribution function \(f_i\), a vector of \(m\) (7 in our case) elements that describe the quantity \(v\) flowing to each neighbour:
\[f_i (x + e_i \Delta x_i, t + \Delta t) - f_i (x, t) = \Omega (x, t)\](14)
where \(t\) is the time; \(\Delta x\) is the spacing of the grid in the direction \(e_i\); \(\Delta t\) is the time step used for the numerical solving; \(e_i\) are the directions of the neighbours (one of theses neighbours being the voxel \(x\) itself); \(\Omega\) is the collision operator.
The left-hand side of eq. 14 represents the diffusion of the quantity \(v\) (streaming step in the LBM jargon) while the right-hand side describe the reaction part (collision step), in our case it corresponds to the chosen ionic model.
The collision step is purely local and can be independently computed for each voxel. In our case, it results in an intermediary value we call \(\frac{dv}{dt}^{*}\) that we compute using a forward Euler scheme following eq. 9. Updating the gating variable \(h\) is also done for each voxel independently and can be seen as a part of the collision step.
Then comes the streaming step where we compute which quantity of \(v\) will stay in place and which quantity will diffuse in each direction. It can be computed by using an intermediate, post-collision state of \(f_i\), noted \(f_i^{*}\), a vector of \(m\) elements for each voxel \(x\). Each element of \(f_i^{*}\) represent a direction \(e_i\) around the voxel, including the “stay in place direction.” \(fi^{*}\) is governed by the multiple-relaxation times approximation (d’Humières 2002) operator:
\[f_i^{*}(x, t + \Delta t) = f_i(x, t) - A(fi - \omega_i v(x, t)) + \omega_i dv^{*}\](15)
where the matrix A relaxes \(f_i\) towards the local value of \(v\) and \(\omega_i\) are coefficient specific to the \(D_nQ_m\) direction discretisation. \(f_i(x, t)\) can then be updated by using the elements of \(f_i^{*}\) that corresponds to the flows towards the voxel \(x\). The quantity \(v(x, t)\) can finally be recovered by the summing the values of the vectors \(f_i(x, t)\).
4.2.2 Anisotropy
In the isotropic diffusion case, \(A = I/\tau\) where \(I\) is the \(m \times m\) identity matrix and \(\tau\) the characteristic relaxation time related to the conductivity of the domain, making it equivalent to the simpler BGK approximation (Bhatnagar, Gross, and Krook 1954).
For the anisotropic case \(A\) must be replaced by \(-M^{-1}SM\) where M projects the vector onto the moment space. From this point we will focus only on the \(D_3Q_7\) case, were \(\omega_0=\frac{1}{4}\) (stay in place) and \(\omega_{1-6}=\frac{1}{8}\) (neighbours). As was done in similar studies (Rapaka et al. 2012; Campos et al. 2016), we consider the first moment as the conserved quantity (\(v\)). The second to fourth moments are related to the flux of \(v\) in directions \(i\) and the remaining moments are obtained using the Gram-Schmidt’s procedure.
\[M = \begin{matrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & -1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & -1 \\ 6 & -1 & -1 & -1 & -1 & -1 & -1 \\ 0 & 2 & 2 & -1 & -1 & -1 & -1 \\ 0 & 0 & 0 & 1 & 1 & -1 & -1 \\ \end{matrix}\]
\[S^{-1} = \begin{matrix} \tau_0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \bar{\tau_{xx}} & \bar{\tau_{xy}} & \bar{\tau_{xz}} & 0 & 0 & 0 \\ 0 & \bar{\tau_{yx}} & \bar{\tau_{yy}} & \bar{\tau_{yz}} & 0 & 0 & 0 \\ 0 & \bar{\tau_{zx}} & \bar{\tau_{zy}} & \bar{\tau_{zz}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \tau_4 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \tau_5 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \tau_6 \\ \end{matrix}\]
\(\tau_0\) is related to \(v\); \(\tau_4\), \(\tau_5\), \(\tau_6\) affects solely the stability of the procedure and were set to 1.33 in our case. Given the anisotropic conductivity tensor components \(\sigma_{ij}\), the other relaxation-time coefficients are given by:
\[\bar{\tau_{ij}} = \frac{1}{2}\delta_{ij} + 4 \frac{\Delta t}{\Delta x_i\Delta x_j} \sigma_{ij} \](16)
where \(\Delta x_i\) and \(\Delta x_j\) are the grid spacing in the \(i\) and \(j\) direction; \(\delta_{ij}\) is the Dirac delta function.
4.2.3 Boundary conditions
Voxels that represent the epicardial and endocardial layers of the domain have no neighbour on at least one of their side. Implementing a no-flux condition on these border voxels is convenient within the LBM framework using the bounce-back rule. This rule consists in imposing an incoming distribution \(f_i\) that is equal to the outgoing distribution in the “no neighbour” direction. A simpler way to phrase this is that these voxels will have other “stay in place” distributions corresponding to the expected outgoing flow in their \(f_i\) vectors.
4.2.4 Implementation
We decided to implement a numerical solver using the LBM taking advantage of the computational power of modern Graphic Processing Units (GPU). Since the collision step is purely local (section 4.2.1) and the streaming step can be expressed using only basic operations such as additions, multiplications and matrix multiplications, GPUs are especially suited and efficient for this type of task.
We used the PyTorch library (Paszke et al. 2019), a high-level python interface for GPU-related operations. While it is mainly developed with deep learning tasks in mind, it provides tensor objects with an interface meant to be very similar to the interface of numpy arrays. Using this type of library alleviates the time required for the development and eases the maintenance of the code but also provides less algorithmic flexibility than using low-level interfaces that are closer to the hardware. In our case specifically, reaching a reasonable computational time implied to not loop “explicitly,” i.e., at the python level, on each voxel but rather use dedicated PyTorch functions where loops are executed in a lower level language, compiled with numerous optimisations.
With cardiac wall segmentations, the 3-dimensional array representing the domain contains a lot of voxels that are out of the domain. Knowing this, we represented the domain as one dimensional arrays of length \(N\) (\(N\) being the number of voxels that are actually part of the domain), one for v, one for h. The main problem that arises with this strategy is that this flat representation does not contain the neighbouring information, which will be required for the streaming step of the LBM. This is why our implementation creates a neighbourhood \(N \times 6\) 2D array, representing the flattened indices of the neighbours in each direction of the \(D_3Q_7\) space and direction discretisation model. When one or several neighbours are outside the domain (this corresponds to the Neumann boundary conditions described in section 4.2.3), we stored the flatten index of the the voxel itself in the corresponding column (C-style, row-major arrays) to easily apply the bounce-back rule. The neighbourhood array only needs to be created once per heart geometry, and is anyway very fast to obtain.
The matrices A (section 4.2.2) were computed once per simulation and stored as a 3D array of shape \(N \times 7 \times 7\). The variables fi, fi_star, dv_star (section 4.2.1) were stored as 2D arrays of shape \(N \times 7\), in relation to the grid model used.
After initialising all elements of fi and v to zeros and those of h to 1, at each iteration of time step \(\Delta t\) (outer loop), the following operations were executed:
Set all columns of
dv_starto the same value: \(dv\) computed with a forward Euler scheme with eq. 9. This is also where we can apply \(J_{stim}\) when needed.Update
fi_starusing eq. 15. Since matrixAis of the right shape and sincevand \(\omega_i\) can be efficiently broadcast by PyTorch, this does not require any explicit inner loop at the python-level.Update
h, also with a forward Euler scheme.Fill the first column of
fiwith the first row column offi_star. This represents the quantity of v that stays in place.Iterate through the rows of the
neighbourhoodarray to update the other rows offiby filling them with the values of the corresponding neighbours, taking advantage of the fast indexing methods offered by PyTorch. This is the only inner loop at the python-level and only increases the running time linearly in regards to the neighbouring scheme chosen (6 in our case) and to the size of the domain \(N\).Update
vas the sum of columns offi.
On a regular grid with a 0.8 millimetres spacing between voxels (\(N\approx 800,000\)), a simulation of 10 seconds of cardiac electrical activity takes about 10 minutes on a nVidia GTX 1080 Ti GPU, using a time step of 0.5 ms.
4.2.5 Conductivity
As explained in section 4.1.2.1, in our simulation framework, the conductivity parameter \(\sigma\) is not the only parameter that influences the apparent speed of the depolarisation wave. Besides \(\tau_{in}\), this speed will also be influenced by the diffusion of neighbouring voxels, which depends notably on the domain topology. Moreover, because the LBM framework, just like other numerical schemes, is an approximation of the mono-domain model of cardiac electrical activity, a null conductivity is not possible because of the phenomenon known as numerical diffusion. In the LBM framework, specifically, a smaller time step \(\Delta t\) increases the strength of numerical diffusion. This is one of the reasons which lead us to choose a time step of 0.5 ms to compute our simulations, since relatively slow speeds are necessary to model re-entrant waves.
In order to calibrate \(\sigma\) to reach target speeds that we defined in section 2, we realised numerical experiments on a \(8 \times 8 \times 0.8\) cm virtual cardiac tissue slab, discretised as a regular grid of \(0.8\) mm of spacing and using a time step of 0.5 ms. In the top left area of \(4 \times 4 \times 0.8\) mm, \(v\) was manually set to 1 to initiate a propagation. The speed of this depolarisation wave was measured as the quotient of the depolarisation time in the bottom left corner minus the depolarisation time outside the area where \(v\) was forced to one by the distance between those 2 points.
This tissue slab was also parameterised to incorporate a “vertical,” top to bottom, fibre direction, so that the speed in the transverse direction could be measured in the top right corner in a similar way.
We empirically established that \(\sigma\) values ranging from \(0.75~mm^2 \cdot s^{-1}\) to \(3~mm^2 \cdot s^{-1}\) in the fibre direction and divided by \(2.5^2\) in the transverse direction yielded apparent propagation speeds compatible with what we used in section 2.
The results of these experiments are shown on fig. 38. However, it must be noted that our tissue slab experiments do not precisely reflects the actual propagation speeds observed with real heart geometries, because their topology will also have an influence on the apparent propagation speed. In particular, thin corridors will be responsible for lower speeds at small thicknesses, as explained at the beginning of this section. That said, these slab experiments were useful to setup a reasonable value for \(\sigma\).
In our real heart geometries, the Streeter model of cardiac fibre orientation (Streeter Jr et al. 1969) was used to generate a set of synthetic fibres. To establish local coordinates and generate these synthetic fibres on voxel data, the solution of the heat equation, also used to compute the wall thickness (section 2.1.2.4), was used as a “wall depth” attribute to each voxel, from 0 in the endocardial layer to 1 in the epicardial layer. The orientation of the major semi-axe of the ellipsoid fitted on the left ventricle (fig. 13) was also used to establish the base to apex direction needed for the Streeter model. We could then used an orientation ranging from -80° (endocardium) to 80° (epicardium). An example of this fibre orientation on a real heart geometry can be seen on fig. 39.
4.2.6 Clustering of simulated VTs
With a high number of inducible pacing sites, it occured frequently that the same re-entrant pattern was induced by different pacing sites. We thus designed an automated, hierarchical clustering strategy to group similar simulations together. Instead of directly defining a distance metric at the voxel level, we decided to use a secondary output of simulations: simulated 12-lead electrocardiograms (ECG) using the dipole formulation (Giffard-Roisin, Fovargue, et al. 2016).
The first step to define our metric was to automatically determine the cycle length (CL) of a simulation output. To this end, we used the following algorithm:
Inputs:
ecg: 2D array of shape \(n\) leads×\(m\) samples
\(min_{CL}\), \(max_{CL}\): minimum and maximum possible cycle length
Output: cycle length (periodicity of the signal)
Procedure:
corrs \(\leftarrow\) empty associative array
for CL from \(min_{CL}\) to \(max_{CL}\) do
..\(s_1 \leftarrow\) ecg[0:end, end-CL:end]
..\(s_2 \leftarrow\) ecg[0:end, end-2CL:end-CL]
..norm \(\leftarrow \sqrt{ \sum_{0}^{m}{s_{1_i}^2} \times \sum_{0}^{m}{s_{2_i}^2} }\)
..corrs[CL] \(\leftarrow \frac{\sum_{0}^{CL}{s_{1_i} \times s_{2_i}}}{norm}\)
end for
return argmax(corrs)
Once the cycle length of a simulated ECG has been determined, we designed a “circular correlation coefficient” and used it to build a a distance matrix between each of our simulated arrhythmia. In the following algorithm, the pad function consits in adding zeros on the right end of an array to allow element-wise operations between 2 arrays of different sizes, and the roll operation consists in shifting elements in the array.
Inputs:
\(s_1\): 2D array of shape \(n\) leads×\(m_1\) samples
\(s_2\): 2D array of shape \(n\) leads×\(m_2\) samples, with \(m_2 \leq m_1\)
Output: circular correlation coefficient
Procedure:
for CL from \(min_{CL}\) to \(max_{CL}\) do
..\(max_{corr} \leftarrow 0\)
..padded \(\leftarrow\) pad(s2, \(m_1 - m_2\))
..norm \(\leftarrow \sqrt{ \sum_{0}^{m_1}{s_{1_i}^2} \times \sum_{0}^{m_1}{padded_i^2} }\)
..for shift from 0 to \(m_1\)
.…rolled \(\leftarrow\) roll(s1, shift)
.…corr \(\leftarrow \frac{\sum_{0}^{m_1}{s_{1_i} \times rolled_i}}{norm}\)
.…if \(corr > max_{corr}\) then
......\(max_{corr} \leftarrow corr\)
.…end if
..end for
end for
return \(max_{corr}\)
Once this distance matrix was computed, we could cluster the results using a standard hierchical clustering algorithm provided by the SciPy toolbox, using \(1 - |corr|\) as the distance metric, and setting a threshold of \(0.05\) to separate the clusters.
4.3 Experiments
4.3.1 Stimulation protocol
To run simulations in our framework, there is one last crucial choice to make: how to “excite,” i.e., initiate the depolarisation wave in our virtual heart? As mentioned in section 4.1, the Mitchell-Schaeffer model does not reproduce any of the autonomic activity of cardiac cells. Moreover we are mostly interested in stimulation and VT induction. This is why we applied a an external stimulation (pacing), to initiate the propagation of a depolarisation wave throughout the virtual heart. Two main elements have to be considered in this regard:
the pacing protocol per se, i.e., the different timings at which the external stimulation will be applied,
the pacing location, i.e., where do we place our “virtual electrode?”
Setting aside the sinusal recordings that are out of scope for our simulation framework, since we did not include any of the complex pathways activated during sinus rhythms (fig. 1), in the clinical EP lab, interventional cardiologists typically record activation maps using 2 families of pacing protocols.
In controlled pacing protocols, the physicians look for abnormal electrograms or abnormally late depolarisation sites to locate zones potentially responsible for arrhythmia. This type of slow pacing, with a stimulation period of usually 600 ms are not expected to induce self-sustained arrhythmias.
In induction protocols, the physicians goal is to induce a self sustained arrhythmia in order to locate (and ablate) the re-entrant channel. These protocols start with an initial controlled pacing phase (called S1) of a few stimulations, after which an earlier S2 stimulation is applied. The first phase is repeated and the S2 timing is reduced at each iteration, until either inducing the arrhythmia or reaching the refractory period. When this S1S2 protocol does not induce any arrhythmia, and if the physician judges that the patient is not too much at risk, this protocol is repeated with a faster S1 phase and/or the physician switches to an S1S2S3 protocol. In a S1S2S3 protocol, the S1 phase is still a controlled, steady pacing, the S2 stimulus is chosen to be just above (generally 20 ms) the refractory period found with the S1S2 procedure, and a third, S3 stimulus is applied in the same way the S2 was applied: by decreasing the S3 interval until either inducing an arrhythmia or hitting the refractory period again.
Concerning the pacing sites, for practical reasons these protocols are usually applied in the endocardial layer of the right ventricular apex. They can also be applied from different sites, at the discretion of the operator, depending on practical settings and its preferences and habits.
In our case, since neither patient safety nor pacing sites accessibility were in play, we chose 101 pacing sites for each patient and conducted complete induction protocols in all of them. The first site was the left ventricular apex, defined by the point where \(\phi\) was minimal (cf section 2.2.2.7). Then we divided the LV in 100 squares for values of \(0.1 < \phi < 2.5\) and \(0 < \theta < \frac{\pi}{2}\). In all of these squares, to maximise the chance for a pacing site to be usable, we picked the point where the thickness was the highest.
At each pacing site, we first started with 6 stimulations spaced out by 600 ms (S1), to allow the virtual heart to enter a steady state. This is necessary because we started our simulations with the gating variable h set to 1 and this would represent a state reached after a theoretically infinite DI. We then conducted S1S2 and S1S2S3 protocols, then restarted the whole procedure using S1=400 ms. At any time during this protocol, if any electrical activity was detected 10 seconds after the last stimulation was applied, the site was marked "inducible" and we recorded the simulated arrhythmia and moved on to the next pacing site.
The pacing stimulations were applied by adding a stimulation current of 2 “normalised potential derivative” to the dv/dt for 10 ms, i.e., 20 time steps, on a zone of minimum 50 voxels around the pacing point.
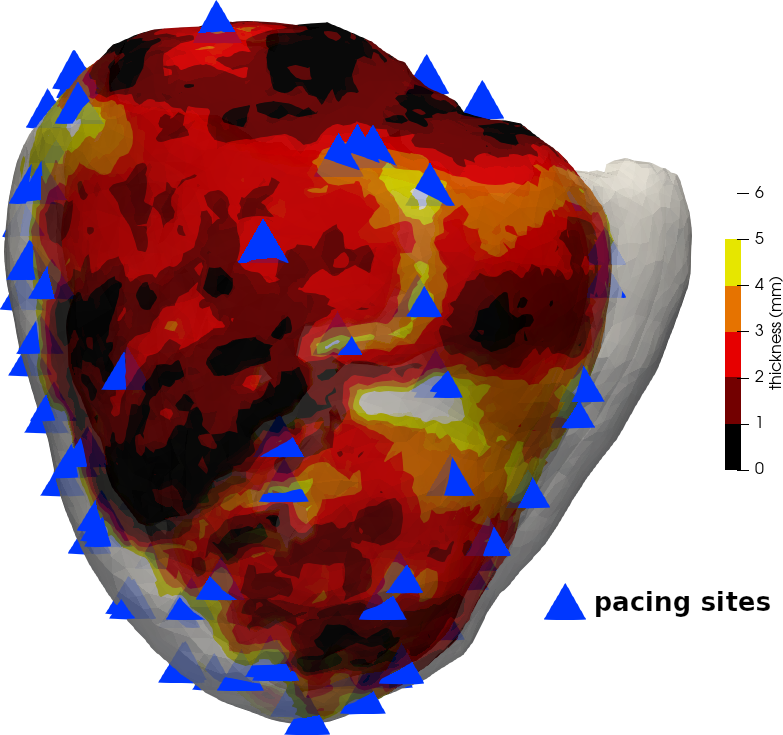
4.3.2 Artificial isthmus
To verify that the chosen parameters could indeed induce VT with inducing protocols, we designed a fake LV with a typical VT CT isthmus similar to what is seen on fig. 11 and described in the literature (Ghannam et al. 2018). This artificial isthmus was created using the MUSIC software9, by coarsely segmenting a real LV epicardium, and designing the endocardium as wanted, using the paint segmentation toolbox, and particularly the repulsor tool that proved very convenient for this task. The resulting artificial isthmus can be seen on fig. 42.
In this fake heart, it was quite easy to induce a re-entrant wave as illustrated in fig. 42 and the associated video. The re-entry induced by the S1S2 protocol can be explained by the fact that the longer refractory period in the scar tissue, consequence of the longer APD, causes the early S2 (or S3) stimulations to not propagate within the isthmus but allows the depolarisation to go around the scar and enter the isthmus from another point. Since the propagation is slowed down within the isthmus, the depolarisation wave can finally excite the voxels that were refractory when they were first hit using the shortest path from the pacing site to the isthmus.
No such re-entrant wave was observed with a steady pacing (600 ms between stimuli) from any site in this geometry. However, from a few sites, a steady but rapid pacing of 400 ms did induce a similar self-sustained arrhythmia.
We also experimented the same pacing protocols but without any heterogeneity in the ionic parameters. No arrhythmia were induced with any protocol or pacing site in this setting, confirming that the heterogeneity in APD is responsible for the arrhythmia here.
4.3.3 On real data
We ran our virtual pacing and induction protocols on 10 different real heart geometries. These patients underwent RFA of VT, so we had activation maps of their VTs recorded during the ablation procedure. All of them underwent injected CTs as part of their pre-procedure routine and we could register CT and EP data using the methodology described in section 2.2.2.7. One full protocol took between 30 seconds and 19 minutes per pacing site (median 6 minutes, standard deviation 2 minutes) on a consumer-grade GPU, depending on whether a self-sustained arrhythmia is easily induced or not.
| theadPatient | No induction by slow pacing | Inducible with dedicated protocol | Documented VT reproduction | Simu CL (ms) | EAM CL (ms) |
|---|---|---|---|---|---|
| 1 | ✓ | ✓ | ✓ | 560 | 507 |
| 2 | ✓ | ✓ | ✓ | 440 | 456 |
| 3 | ✓ | ✓ | ✓ | 560 | 410 |
| 4 | ✓ | ✓ | \(\times\) | - | 560 |
| 5 | ✓ | ✓ | ✓ | 320 | 260 |
| 6 | ✓ | ✓ | ✓ | 420 | 370 |
| 7 | ✓ | ✓ | ✓ | 580 | 446 |
| 8 | ✓ | ✓ | ? | - | - |
| 9 | ✓ | \(\times\) | \(\times\) | - | - |
| 10 | ✓ | ✓ | ? | - | - |
Slow pacing (S1=600 ms) did not trigger any self-sustained arrhytmia in any of the 101 pacing sites in any patient. In 9 out of 10 patients, it was possible to induce at least one simulated VT using a dedicated protocol. For 6 patients, one the simulated VTs matched either the recorded VT or its mirror pattern. In one patient, it was not possible to induce any VT using the global parameterisation scheme we described above. Cycle lengths of the simulated VTs, while in the correct order of magnitude, differ substantially than their real data counterparts.
For the following paragraphs, we strongly advise the reader to visit the associated website at link, where 3D interactive views of the simulations are visible within the web browser.
4.3.3.1 Patient 1
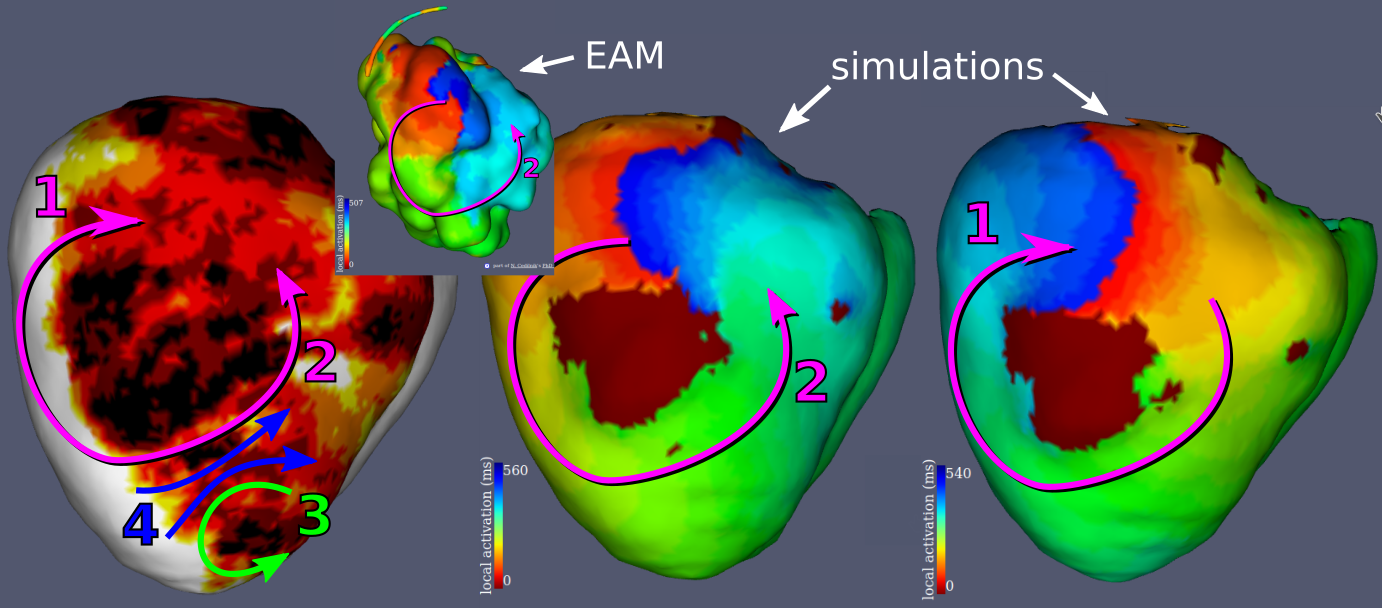
For patient 1, 14 pacing sites resulted in a simulated VT for a total of 7 different patterns. The recorded EAM was matched in both the forward (counter-clockwise) and backwards (clockwise) directions, with a slightly longer cycle length in the simulations.
4.3.3.2 Patient 2
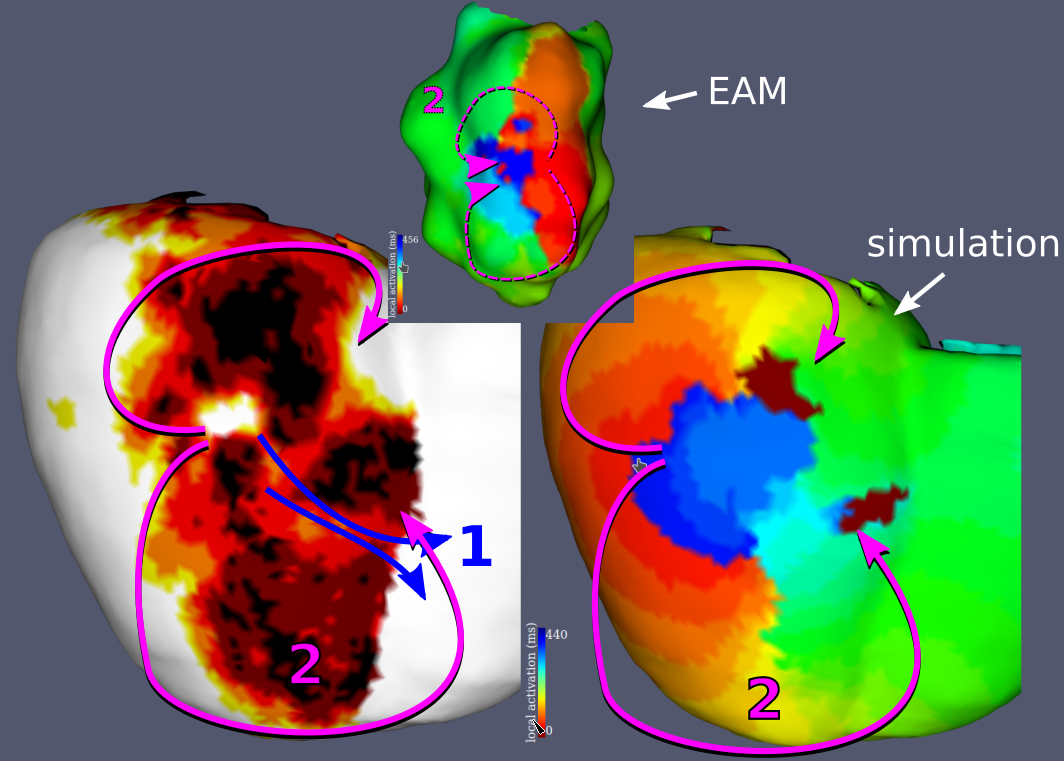
For patient 2, 11 pacing sites were inducible for a total of 3 different re-entrant patterns after clustering. Only the mirror reflection of the documented pattern, a typical figure of eight, was matched. In the other simulated VTs took, the depolaristaion wave goes through similar channels, but in a simpler rotating pattern.
4.3.3.3 Patient 3
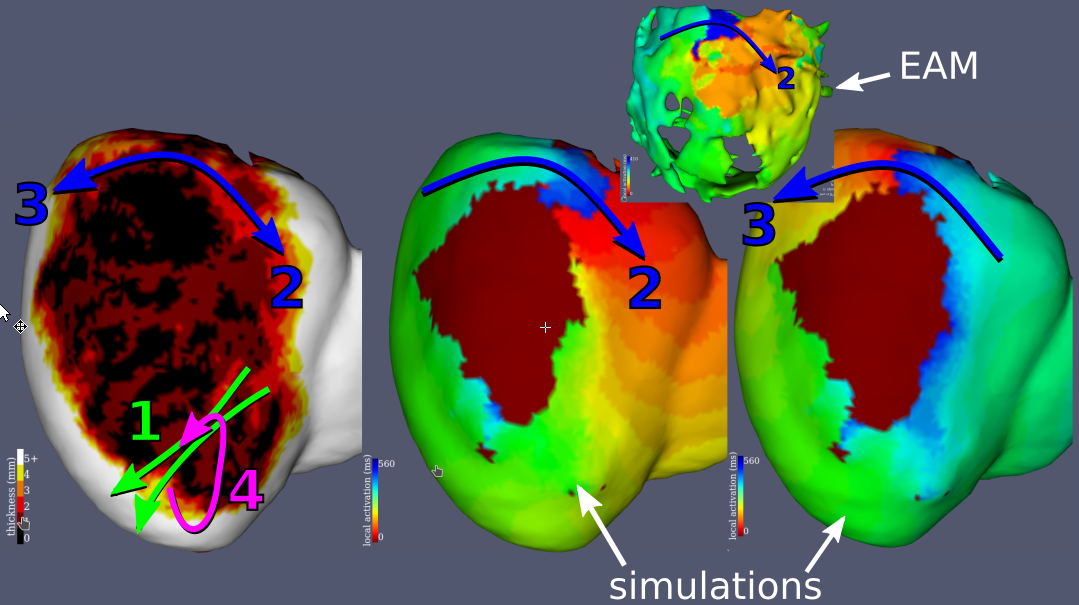
For patient 3, 22 sites were inducible for a total of 4 different activation patterns. As for patient 1, the recorded pattern was matched both in the same and reverse direction. However, the simulated VTs have a longer CL than the recordings: 560 vs 410 ms.
4.3.3.4 Patient 4
For patient 4, 9 sites were inducible for a total of 5 different activation patterns. Only the simple patterns are represented on the figure above. For this patient, the recorded VT was not match by any of the simulated VTs.
4.3.3.5 Patient 5
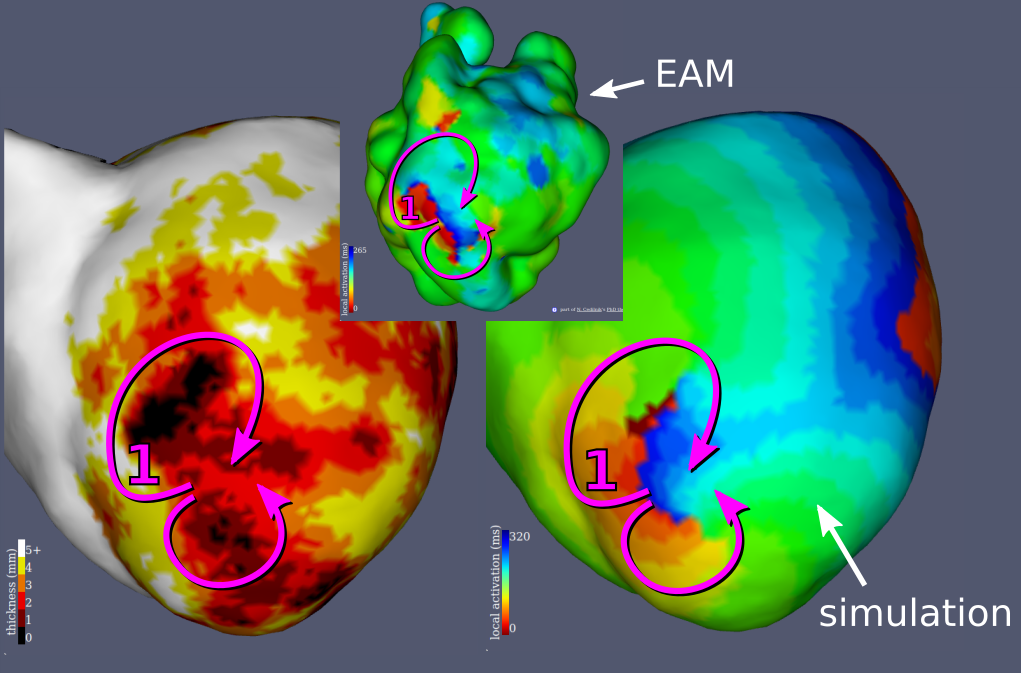
For patient 5, 6 sites were inducible for a total of 3 different activation patterns. We only represented the pattern that matched the recording on the figure above because the other patterns are not visible from this point of view.
4.3.3.6 Patient 6
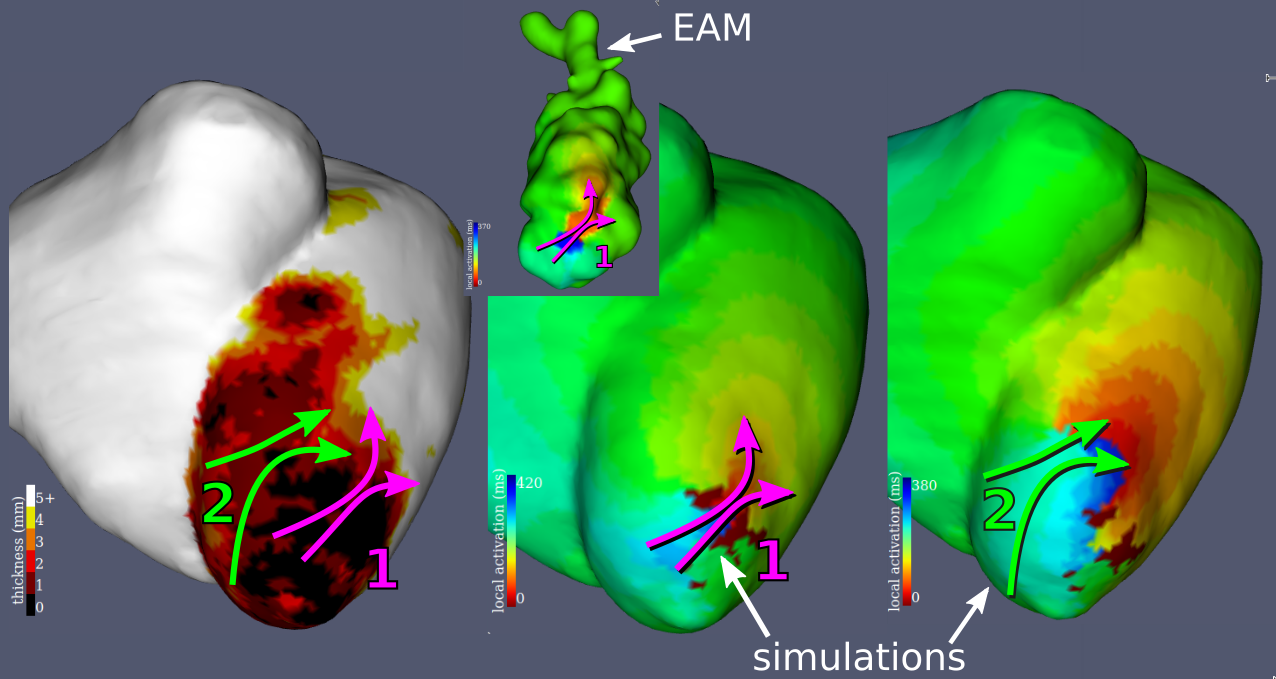
For patient 6, 27 sites were inducible for a total of 2 different activation patterns, one of them clearly matching the recorded figure of 8 pattern.
4.3.3.7 Patient 7
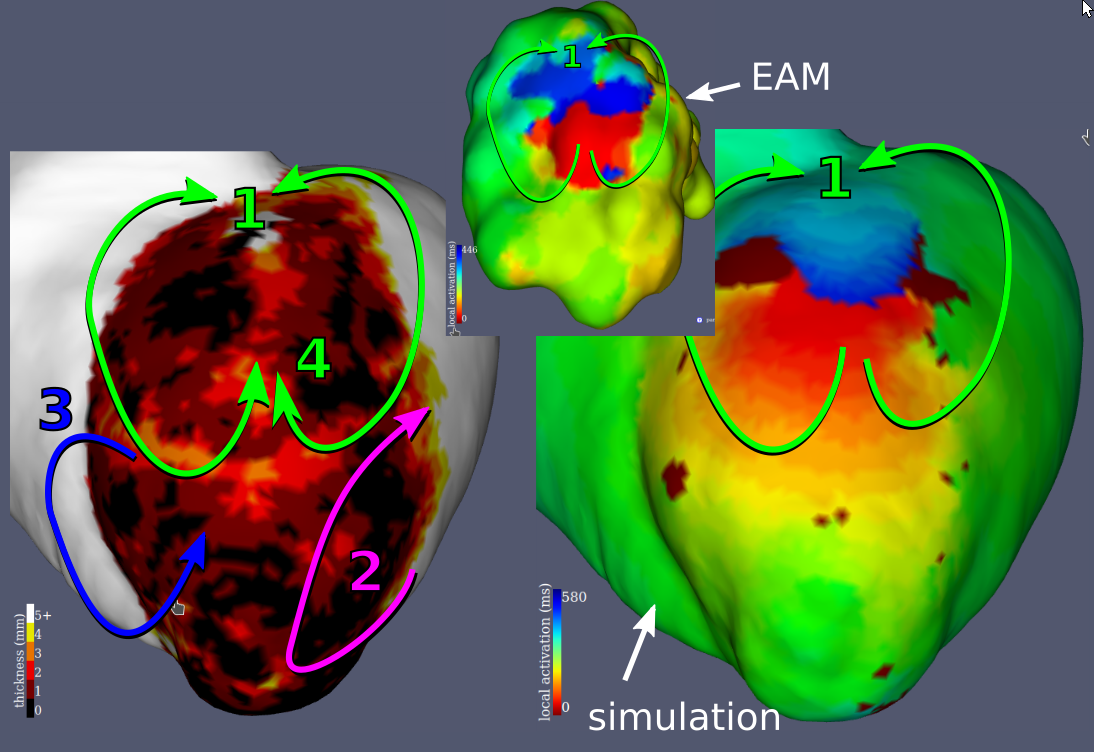
For patient 7, 68 sites were inducible for a total of 10 different activation patterns. It is by far the most inducible heart in our database. As for patient 1 and 3, the recorded VT was matched both in the same and reverse direction by our simulations.
4.3.3.8 Patient 8
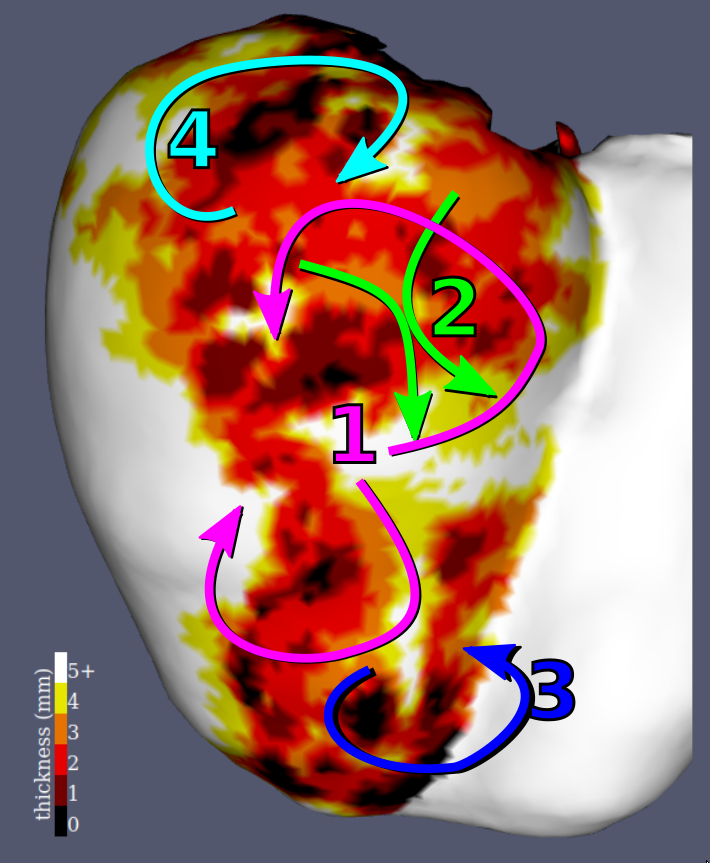
For patient 8, 7 sites were inducible for a total of 5 different activation patterns. For this patient, it is unclear whether of one these patterns match the recordings because of the EAM’s poor resolution and registration uncertainties.
4.3.3.9 Patient 9
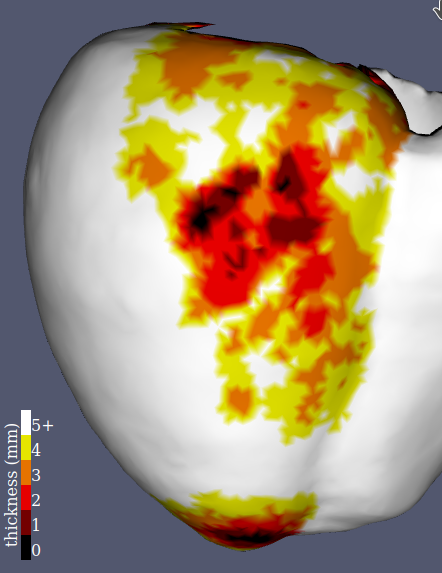
Patient 9 is the only patient that did not present any self-sustained arrhythmia in our simulations.
4.3.3.10 Patient 10
For patient 10, 18 sites were inducible for a total of 3 different activation patterns.
4.4 Discussion
We showed that our personalised models are able to reproduce documented re-entrant VTs, only based on CT imaging features. Not all documented VTs could be reproduced, but in most cases where they could not, we believe it is due to CT/EP registration errors and/or missing/interpolated EP data by the EP lab catheter console. Expecting to reproduce all known VTs for a patient in our framework does not seem like a reasonable goal anyway, since we do not expect to be able to incorporate into our models all the complex modifications of the scarred myocardium. Nonetheless, there are some areas where our simulations could and should be improved by future work.
4.4.1 Limitations
First, our virtual hearts are a little too excitable: induction protocols in real life have lower success rates than our virtual ones. But our virtual protocols are also far more aggressive than what is doable when patient safety is a limiting factor, so this hyper-excitability must not be interpreted as an argument for the complete dismissal of our satisfying results.
Secondly, our simulated VTs, even when reproducing documented activation pattern, have a different cycle length than their real-life counterparts. It seems possible to adjust our parameterisation such that all simulated VTs are shorter, unfortunately the CL discrepancy does not seem to obey to a simple constant or linear relationship. On a related note, in our simulations refractory periods are often hit around 300 ms while real cardiac tissue is generally expected to tolerate higher paces.
4.4.2 Possible improvements
As mentioned earlier, we treated the physiological thinning of the basal area of the left ventricle by an ad hoc modification of the excitability parameter. We would like to design a more subtle way of incorporating this natural thinning, and we probably also need to address the natural thinning of the apex in a similar way. We believe that the VT of patient #6, which is almost twice slower in our simulations than in the intra-cardiac recording and uses a near apical VT isthmus, is a strong argument to refine our relationship between thickness and model parameters. This should be easily integrated using the spherical coordinate \(\phi\) described in section 2.2.2.7.
Finally, the pacing sites selection strategy described in section 4.3.1 can be refined. It is possible that our simulations can induce arrhythmias more selectively by using the channelness filter described in section 2.2 to select pacing sites. The precise parameters and/or adaptation of this filter for this task, and the pacing point choice strategy that would derive from its use still needs to be studied.
5 Conclusion
5.1 Contributions
5.1.1 Eikonal model personalisation
In section 2.1, we demonstrated that there was a relationship between CT LV wall thickness and depolarisation wave front apparent propagation speed during VT.
We extended this relationship to controlled pacing maps in section 2.2.3.3.
In section 2.1.3, we proposed a methodology to model electrical refractoriness in Eikonal models: the unidirectional conduction block.
In section 2.4.2.2, we proposed a methodology to identify apparent propagation speeds on intra-cardiac electro-anatomical maps using Eikonal models. This methodology is linked to an approach to identify initial depolarisation sites (section 2.4.4) on these maps that usually do not cover all heart surfaces.
We proposed a fast electrogram simulation model with a formulation combining the Eikonal model to an AP model in (section 2.3.3.4).
5.1.2 Mono-domain model personalisation
In section 4.1.2, we built a mono-domain cardiac electrophysiology model personalisation framework based on CT imaging based on the results obtained in section 3.4.2.
In section 2.1.6, we present an efficient implementation of the lattice Boltzmann method for cardiac EP leveraging on the computational power of graphical processing units without needing to resort to low-level programming languages.
In section 4.3, we showed that our mono-domain simulations were able to reproduce documented VTs using in silico versions of induction protocols that interventional cardiologists use during radio-frequency ablations.
5.1.3 Signal and image processing
5.1.3.1 Cardiac imaging
In section 2.3.2.1, we proposed a deep learning approach to segment the myocardial wall on high resolution three-dimensional CT images.
In section 2.2.2.7, we developed a “left ventricular spherical coordinates” suited for multi-modal data integration.
In section 2.2.2.6, we introduced a channelness filter to identify potential VT isthmuses on CT images.
5.1.3.2 Unipolar electrograms
In section 3.2.3, we proposed the “adaptative plateau finding” algorithm to determine the start and the end of the depolarisation complex on unipolar electrograms.
In section 3.2.4.2, we described an algorithm to discriminate positive, negative and biphasic depolarisation waves on unipolar electrograms.
Using these algorithms, we established a relationship between CT wall thickness and action potential duration in section 3.4.2.
5.2 Publications
The following articles are directly related to the topic of this PhD and were reproduced in section 2
The following articles were redacted during the time of this PhD. They illustrate the numerous collaborations we could be part of during this PhD, but were only mentioned in this manuscript, as they are not directly linked to model personalisation.
5.3 Conclusion
We have shown throughout this manuscript that computed tomography measured left ventricular wall thickness is a valid support for patient-specific cardiac electrophysiological model personalisation in chronic myocardial infarction patients. Most of the the similar studies rely on late gadolinium enhancement magnetic resonance imaging, which main advantage is a contrast between healthy and fibrotic myocardium. We believe that with its better reproducibility and higher resolution, allowing to overcome the classical grey zone/dense scar dichotomy and map infarct scar with a finer level of details, CT imaging is an interesting modality in such context.
In section 2, we showed that slower wave front propagation in thinner areas was sufficient in many cases to reproduce ventricular tachycardia activation patterns recorded during catheter interventions. Surmounting the limitations of Eikonal models by using more sophisticated models in section 4, we showed that electrical restitution properties could also be parameterised according to wall thickness, motivated by experimental data in section 3 and validated by the simulation experiments of section 4.3.
5.4 Discussion
To our knowledge, it is the first time that the lattice Boltzmann method for cardiac electrophysiology has been used in the context of model personalisation for ischaemic VT based on medical imaging. This is surprising, knowing the convenient transition from medical imaging features to parameters for this method because both are represented in a regular grid, a 3D image, in silico. This characteristic of the lattice Boltzmann method also makes it particularly adapted to ongoing work combining physical models and neural networks. In fact, the implementation we developed during this PhD has already been used for a preliminary study (Ayed et al. 2019) on this topic.
Our goal was to build a model personalisation framework using non invasive data, yet in section 4.1.2, we indirectly used results obtained using invasive data in section 3. Nevertheless, unlike the inspirational work for this thesis (Relan 2013), the EP data was never used to tailor parameters for a specific patient directly, but rather as a gateway from imaging features to CT images.
5.5 Perspectives
Our future work will focus on refining the reaction diffusion model parameterisation.
Besides the precious information provided by wall thickness, it is probably valuable to incorporate fat infiltration information (De Coster et al. 2018), which can be easily extracted from CT images. We also believe that other sources of non invasive data will prove useful for the personalisation process. At the very least, we will investigate whether 12-lead electrocardiograms could be useful to tailor propagation speeds and/or repolarisation characteristics to a patient physiology. Since most target patients are already wearing an implantable-cardioverter defibrillator that record their cardiac activity, it would be a pity not to investigate how these recordings may be used. Connected devices such as smart watches are also an option here, although their reliability is still debated (Koshy et al. 2018).
Improving information extracted from the electro-anatomical maps should also prove very useful to improve our personalised simulation framework. As can be seen in the VT recordings shown in this manuscript, many aberrant data points remain present in the electro-anatomical maps, even when considering the supposedly easy task of detecting the depolarisation time. This is in part explainable because these maps are created in real time in the cardiac intervention room. Using more computationally intensive algorithms to rebuild activation maps should give us better “ideal” goals for the output of our simulations.
We limited our experiments to patients who were referred to the rhythmologists for VT episodes. Thus we cannot evaluate whether our personalised simulations are able to stratify the arrhythmia risk in the general infarcted populations. This is another axis we wish to lead our future investigations to.
Image integration in catheter ablation procedures have already improved the intervention process. We advocate that personalised simulations before entering the catheter lab represent the next step of precision medicine in rhythmology. Future ablations using non-invasive radiotherapy approaches have already shown encouraging results (Cuculich et al. 2017). Since no intracardiac exploration phase is possible with these methods, personalised simulations could be helpful to bridge the gap between catheter and radiation ablation of arrhythmias.
Bibliography
Whether evolutionary selected processes should be considered optimal or not is a fascinating question but unfortunately out of the scope of this thesis.↩︎
This variation on “all models are wrong” is from Paul Valéry in Mauvaises pensées et autres, Éditions Gallimard (1942)↩︎
For didactic purposes, we will now use the term ion channels to designate ion channels and transporters indistinctly.↩︎
Only a few models are given as examples here; an exhaustive review including a proper classification of the the different cardiac AP models available in the scientific literature could probably constitute a thesis on its own.↩︎
“virtual cells” actually represent groups of cells rather than individual myocytes↩︎